作者:谢正泰、樊佳亮、刘 梅、金 龙
来源:信息与控制
编辑:董亚微@一点人工一点智能
原文:基于神经网络的机器人学习与控制:回顾与展望
机器人因其高效的感知、决策和执行能力,在人工智能、信息技术和智能制造等领域中具有巨大的应用价值。目前,机器人学习与控制已成为机器人研究领域的重要前沿技术之一。各种基于神经网络的智能算法被设计,从而为机器人系统提供同步学习与控制的规划框架。首先从神经动力学(ND)算法、前馈神经网络(FNNs)、递归神经网络(RNNs)和强化学习(RL)四个方面介绍了基于神经网络的机器人学习与控制的研究现状,回顾了近30年来面向机器人学习与控制的智能算法和相关应用技术。最后展望了该领域存在的问题和发展趋势,以期促进机器人学习与控制理论的推广及应用场景的拓展。
机器人被誉为20世纪人类最伟大的发明之一。它具有感知能力、决策能力和执行能力,能够协助甚至替代人类完成各种复杂、繁重和危险的任务。任何涉及重复性工作的工业系统都可以通过机器人实现自动化作业,进而在降低人力成本的同时显著地提高生产效率和产品质量。这也预示着现代智能工厂能够根据需求扩大或缩小生产规模。典型的机器人设备包括冗余度机器人、柔性机器人和移动机器人等。近年来,机器人在军事战争、太空探索、医疗手术和其他重要行业中得到了广泛的应用。
在第四次工业革命的推动下,机器人系统,特别是机械臂,受到世界各国的广泛关注。机器人技术与多学科技术相结合,逐步推动了人类社会生产和生活方式的转变。以机器人视觉和触觉为代表的机器人感知技术加速了机器人学习与控制概念的产生和发展。因此,机器人系统能够克服源于自身或环境的不确定性因素,从而提高任务执行的效率和稳定性。具体而言,机器人需要解决由磨损、老化、故障等因素引起的结构不确定性问题和由环境、任务等因素决定的决策问题。因此,亟需开发其自我学习和实时校准功能。近年来,相关的学习技术提高了具有不确定性的机器人系统的容错能力和决策能力。另一方面,在任务执行过程中,机器人期望保持稳定且高效的工作性能。因此,它需要基于特定的控制方案和高效的网络算法以实时获得合适的控制信号。这要求机器人系统具备优越的容错能力和可靠的控制精度,并在此基础上以人工智能的模式实现复杂多变的任务。
近年来,脑机接口技术、手术机器人、康复机器人、多机器人集群等新兴概念的发展对机器人控制技术与应用提出了实时性、精确性、稳定性、容错性、鲁棒性等多方面实际要求。随后出现了一系列先进的控制技术,如远中心控制、视觉伺服控制、模型预测控制、阻抗控制。因此,探索机器人学习与运动控制相结合的新模式是近年来国内外机器人研究的重点。
基于神经网络的机器人学习与控制技术已成为前沿科技之一,也是智能制造、智慧医疗和无人驾驶领域中的重要瓶颈技术之一。近30年来,相关的研究成果显著地提高了机器人系统的功能性、精确性和智能性。机器人学习技术利用数据驱动方法分析、预测和估计带有不确定性的模型或策略;机器人控制技术结合学习信息与控制算法实现功能性运动规划。在多源传感器的协助下,机器人系统可以收集、处理和开发数据,进而集成数据库,甚至搭建数据云。随后,基于神经网络的机器人算法根据测量数据实现优化的学习与控制过程。
神经网络具备强大的拟合能力和并行处理能力,可以被理解为机器人的“大脑”。面向机器人学习与控制的主流神经网络方法包括神经动力学 (neural dynamics,ND)方法、前馈神经网络 (feedforward neural network,FNN)方法、递归神经网络(recurrent neural network,RNN)方法和强化学习(reinforcement learning,RL)方法。ND方法通过构建常微分方程(ordinary differentialequation,ODE)形式或对应的离散变体系统以求解机器人学习与控制问题,并实现实时参数辨识和机器人控制。FNN方法属于一种机器学习算法,能够通过更新权值逼近机器人系统的特定函数,从而开发相应的数据驱动技术。与FNN方法不同,RNN方法的网络节点之间可以构建循环连接,允许一些节点的输出影响其后续输入,在机器人学习领域有显著的应用价值。值得注意的是,ND方法和RNN方法在结构上存在交集。当ODE形式的计算网络的输入神经节点数大于或等于2时,该系统即属于RNN方法,也可被称为ND方法。为了便于阐述,本文分别对ND方法与RNN方法进行单独介绍。RL方法能够解决机器人与环境交互过程中的决策问题,并通过试错的方式实现机器人特定技能的学习。
以上4种机器人学习算法均属于人工智能算法的范畴。其主要任务是开发智能信息处理应用,从而设计与人类智能相似的机器人系统。在真实场景中,机器人的交互过程产生的学习与控制问题通常需要多种技术协同解决。这要求机器人系统通过传感器获取大量的测量数据,进而驱动学习和控制过程。因此,机器人学习与控制系统的发展必然伴随着传感器技术、神经网络方法、数学理论等重要技术的进步。
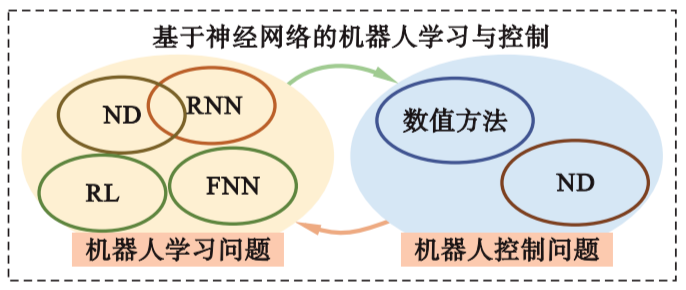
如图1所示,本文回顾了用于解决机器人学习与控制问题的神经网络方法以及相关应用,其中,机器人学习包括机器人模型学习和机器人策略学习两个方面。相关的神经网络方法被归纳为ND方法、FNN方法、RNN方法和RL方法。
本节介绍了机器人运动学模型、动力学模型和决策模型,并说明了机器人系统的学习与控制问题。
常用的机器人模型包括机器人运动学模型、动力学模型和决策模型。机器人运动学模型在机器人控制中扮演着至关重要的角色,是机器人轨迹规划、运动控制、视觉伺服等重要功能的实现基础。机器人运动学包括机器人正运动学和机器人逆运动学。对于一个n 自由度的机器人而言,其正运动学模型为T(\theta)=p ,式中,\theta \in \mathbb{R}^n 表示机器人的关节角度向量;p\in \mathbb{R}^m 表示机器人的末端执行器位姿向量;\pmb{T}(·):\mathbb{R}^n \rightarrow \mathbb{R}^m 表示非线性映射函数。此外,速度层运动学模型为\pmb{J(\theta,\phi)}_k\pmb{\dot\theta}(t)=\pmb{\dot p} ,式中,\pmb{\dot{\theta}} 表示机器人的关节速度向量;\pmb{\dot p}(t) 表示末端执行器的笛卡儿速度向量;\boldsymbol{J}\left(\boldsymbol{\theta}, \boldsymbol{\phi}_{k}\right)=\partial \boldsymbol{T}(\boldsymbol{\theta}) /\partial \boldsymbol{\theta} \in \mathbb{R}^{m \times n} 表示机器人的雅可比矩阵;\pmb{\phi}_k \in \mathbb{R}^h 表示由运动学参数组成的常数向量。
与机器人运动学不同,机器人动力学模型不仅与关节速度、关节加速度等运动学变量有关,还涉及机器人系统的质量、惯性、外部受力等因素。机器人动力学阐述了机器人驱动力/力矩与机器人运动状态之间的关系。对于一个n自由度的机器人而言,其关节空间的动力学模型为\boldsymbol{M}(\boldsymbol{\theta}) \ddot{\boldsymbol{\theta}}+\boldsymbol{C}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}}) \dot{\boldsymbol{\theta}}+\boldsymbol{g}(\boldsymbol{\theta})=\boldsymbol{\tau}+\boldsymbol{J}^{\mathrm{T}} \boldsymbol{f}_{\mathrm{e}},式中,\boldsymbol{M}(\boldsymbol{\theta}) \in \mathbb{R}^{n\times n} 被定义为惯性矩阵;\ddot{\boldsymbol{\theta}} \in \mathbb{R}^n 表示机器人的关节加速度向量;\boldsymbol{C}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}}) \in \mathbb{R}^{n \times n} 表示科氏和离心矩阵;\boldsymbol{g}(\boldsymbol{\theta}) \in \mathbb{R}^n 表示重力向量;\boldsymbol{\tau} \in \mathbb{R}^n 表示机器人的关节扭矩向量;\boldsymbol{f}_{\mathrm{e}} \in \mathbb{R}^m 表示施加在末端执行器的力。机器人的决策模型可以用马尔可夫决策过程来表述,它由(S,A,P,R,\delta) 五个部分组成,其中,S 表示环境状态空间/集合,s \in S 表示具体状态;A 为机器人的动作空间/集合,a \in A 为具体动作;P(s'|s,a) 表示机器人在执行动作a 的状态下到达下一个状态s' 的转移概率分布函数;R 表示奖励函数,r(s'|s,a)\in R 表示机器人在状态s 下执行动作a 以到达状态s' 时获得的即时奖励;\delta \in [0,1] 表示折扣因子,能够在计算累积奖励时削弱未来奖励的影响。在执行策略阶段,机器人在当前状态s_t (t 表示当前时刻)依据策略\pi 执行动作a_t得到奖励r_{t+1} ,并根据状态概率分布函数P(s_{t+1}|s_t,a_t) 到达新状态s_{t+1} ,直到机器人到达终止状态。
基于模型的运动学控制方法(如伪逆法、模型预测控制等)都是在运动学模型框架上设计的。在机器人系统中,运动学模型可以由机器人的Denavit-Hartenberg参数确定,这取决于机器人的出厂参数设置。然而,由于诸如磨损、老化、故障等因素,机器人结构参数(例如雅可比矩阵)可能发生变化。因此,机器人运动学中不可避免地存在不确定因素。与此同时,机器人的硬件设计与开发过程也会增加模型的不确定性。基于模型的运动学控制方案难以精确控制此类具有不确定性的机器人,这可能显著地降低机器人系统的任务执行性能。对于机器人的动力学模型而言,多个动力学参数、外部负载和其他因素(如难以辨识的摩擦力)会增加其不确定性。此外,对于多自由度机器人手臂,各关节的运动会引起机器人的质量分布、惯性矩大小、力臂长度等参数的改变,进而显著影响其动力学结构。其次,机器人系统存在时间延时特性,例如,因周期性采样导致的单位时延,以及因系统机电部分的惯性导致的时间滞后。再者,传感器测量误差、建模误差和噪声影响给机器人系统的动态控制带来了很大的困难。上述不确定性情况均被归纳为机器人模型学习问题。
机器人学习的另一个重要研究方向是机器人策略学习。不同于机器人模型学习,机器人策略学习的目标是求解马尔科夫决策过程的最优策略\pi^*(a|s) 以指导机器人运动,并实现最大化折扣累积奖励U_t=\sum_{k=t}^{\infty}{\delta}^{k-t}r_k 。这种建模方式给机器人策略学习提供了一个具有通用性和可移植性的系统框架。在此框架中,机器人策略学习问题涉及定义状态空间、环境模型、运动策略模型等。机器人强化学习算法在给定状态空间的前提下学习运动策略模型,而环境模型通常是未知的。强化学习会通过与环境交互进行试错学习,并以此为基础进行策略优化。机器人策略学习能够克服机器人与环境交互过程中的不确定因素,从而提高系统功能性和智能性。
探究基于学习技术的机器人控制器与方案求解器,继而建立具有通用求解性能的智能控制系统,是机器人技术开发中的另一个难题。首先,针对具备不确定性的机器人系统,需要对不确定性参数进行有效学习,并且在学习的同时将所学知识传递给控制系统。输出的控制信号在控制机器人的同时反馈于学习系统进行同步参数学习。如此学习与控制结合的迭代循环需要在给定的采样间隔内完成,以满足机器人系统的实时性要求。此外,随着系统的功能性需求提升,机器人控制算法需实现诸如稳定性优化等功能。再者,智能机器人系统可能存在诸如雅可比矩阵奇异、所构建的控制模型非凸、噪声干扰等棘手问题。上述3个方面被归纳为机器人控制问题,严重制约了系统的高效控制。
面向机器人系统的学习与控制问题,下文将重点介绍以ND方法、FNN方法、RNN方法和RL方法为代表的神经网络技术以及相关的应用。
ND方法是一种基于数据驱动技术且无需训练的实时求解算法。它通过开发具有全局收敛特征的ODE系统或对应的离散变体系统以不断减小系统误差。当ND方法的输入变量大于或等于2时,ND方法属于RNN方法的特殊形式,能够解决机器人学习与控制、矩阵求逆等问题。单变量ND算法的应用包括时变非线性方程求解。
以雅可比矩阵学习为例,ND算法的学习目标为实现\pmb{\hat{J}\dot{\theta}=\hat{\dot p}\rightarrow \dot p} 或\pmb{\hat{J}\rightarrow J} ,其中\pmb{\hat J} 表示估计的雅可比矩阵;\pmb{\hat{\dot p}} 表示末端执行器的估计速度。这个参数学习问题可从优化的角度转化为最小化问题,并设计误差函数\pmb{\varepsilon =\hat{\dot p}-\dot p=\hat{J}\dot \theta-\dot{p}} 。ND算法通过构造收敛系统以求解该最小化方案。其它基于ND算法的机器人学习技术也类似以上过程。为了便于理解,图2提供了基于ND方法的机器人系统结构图。如图所示,传感器系统将机器人状态数据传递给由神经动力学算法和机器人控制系统组成的计算网络。测量数据难免会受到噪声和误差等因素影响,网络的输出经过数据滤波系统后,作为控制信号输入用于执行任务的机器人系统。此后,机器人状态数据被传感器系统再次测量,使得整个系统进入一次新的循环。这样持续的循环过程实现了机器人系统的学习与控制。
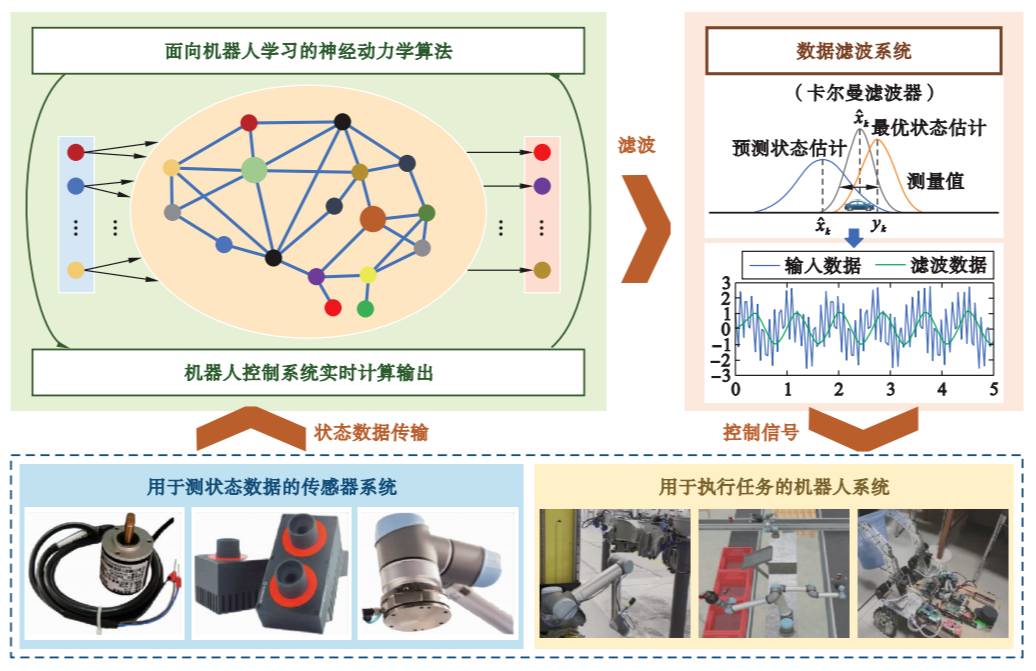
Broyden算法是一种有效求解非线性系统的拟牛顿法,已广泛应用于机器人学习中。Broyden算法仅在第1次迭代时计算雅可比矩阵,在后续迭代中进行参数更新。基于Broyden算法,文[49-50]设计了面向机器人系统的动态和静态离散时间学习公式:
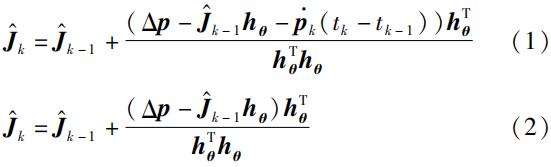
式中,\Delta \pmb{p} =\pmb{p}_k-\pmb{p}_{k-1} ,\pmb{h_{\theta}}=\pmb{\theta}_k-\pmb{\theta}_{k-1} ,下标k 和k-1 表示第k 和k-1 时刻。基于Broyden方法的静态离散时间学习公式(2)相对于动态式(1)去除了速度项\pmb{\dot{p}}_k(t_k-t_{k-1})\pmb{h_\theta}^T 。在跟踪静态目标或极小采样间隔的情况下,式(1)和式(2)的学习性能是类似的。然而,对于动态目标,式(1)能够获得更小的学习误差并取得更好的收敛性能。此外,面向机器人模型不确定的情况,该方法需要传感器获得真实末端执行器的笛卡儿速度\pmb{\dot{p}}_k 来促进雅可比矩阵的学习。基于Broyden方法的机器人学习公式(1)和学习公式(2)多次被应用于处理未标定机器人视觉伺服问题。文[51]基于Broyden方法和测量数据在线估计了视觉雅可比矩阵,进而实现了无模型视觉伺服的任务模式。文[52]针对机器人与未知弹性物体相互作用的问题,提出了一种基于视觉的变形控制器,利用视觉反馈实时估计变形后的雅可比矩阵,避免了繁琐的传统模型辨识步骤。值得注意的是,上述学习公式需要与控制算法进行结合以实现机器人系统的同步学习与控制。虽然Broyden方法在机器人参数估计中是有效的,但是其收敛速度主要取决于机器人的状态且无法调整。
近年来,零化神经动力学(zeroing neural dynamic,ZND)算法被设计以收敛误差函数\pmb{\varepsilon} ,进而解决机器人系统的无模型控制问题。该算法最初开发神经动力学模型\pmb{\dot{\varepsilon} =-{\mu}\varepsilon} (其中\mu>0 为收敛参数)构建ODE形式的收敛系统。例如,文[28]基于ZND算法和伪逆法构造了机器人雅可比矩阵的学习算法:
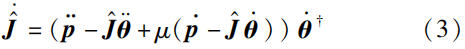
式中,\pmb{\dot{\hat{J}}} 为\pmb{\hat{J}} 的时间导数;\pmb{\ddot{p}} 表示末端执行器的笛卡儿加速度;上标\dagger 表示向量或矩阵的伪逆且\pmb{\dot \theta}^\dagger=\pmb{\dot \theta}^T/(\pmb{\dot \theta}^T\pmb{\dot \theta}) 。当关节速度等于零向量时,\pmb{\dot \theta}^\dagger 会陷入奇异状态。为了避免该问题,奇异状态下的关节速度的伪逆形式被其转置形式所取代。此外,式(3)要求从外部传感器获取末端执行器的笛卡儿速度和加速度的实时信息。文[28]中的理论分析表明,由式(3)生成的误差函数\varepsilon 满足\pmb{\varepsilon}(t)=\pmb{\varepsilon}(0)\text{exp}(-\mu t) 。换言之,误差函数\pmb{\varepsilon} 能通过对\pmb{\hat{J}} 的实时更新全局收敛于零向量。后续的拓展研究基于式(3)开发了意图识别应用和离散学习公式研究,进一步验证了该学习算法的可行性。此后,文[55]提出了一个附带积分项和激活函数的机器人学习公式:
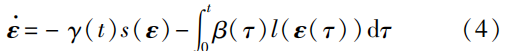
式中,\gamma(t)>0 和\beta(t)>0 表示时变收敛参数;s(·) 和l(·) 表示激活函数。文[55]借助额外的视觉传感器实时获取末端执行器状态数据,并给出了详细的机器人实验验证。此外,文[55]的理论证明显示,式(4)的误差\pmb{\varepsilon} 能在噪声的干扰下实现有限时间收敛。
然而,上述ZND研究预先假设了未知雅可比矩阵满足某些结构特性。这些先验信息在实际应用中通常很难获得。其次,ZND方法估计的雅可比矩阵\pmb{\hat{J}} 与实际雅可比矩阵\pmb{J} 是有区别的。其原理在于引导末端执行器的估计速度接近实际速度。换言之,ZND方法实现了误差函数\pmb{\varepsilon=\hat{\dot{p}}-\dot{p}} 趋近于零向量,而不是雅可比矩阵估计误差\pmb{\hat{J}-J} 趋近于零矩阵。此外,不同ND方法的比较结果被总结在表1中。

注入必要的随机噪声\pmb{n} 能够促进估计的雅可比矩阵\pmb{\hat{J}} 根据近几年的研究发现,在机器人学习算法中的学习过程。随机噪声\pmb{n} 可能源于真实场景中的计算误差、测量误差、环境噪声等方面。LI等基于梯度下降法提出了噪声驱动的学习算法:
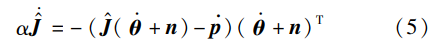
式中,\alpha >0 表示收敛参数。附加噪声\pmb{n} 能够丰富学习算法的输入多样性,可以被视为一种数据增强形式。对此,文[56]在理论上证明了雅可比矩阵学习误差\pmb{\hat{J}-J} 能够全局收敛于零矩阵。相比之下,不添加噪声而仅基于梯度下降法的学习算法无法学习准确的雅可比矩阵。由此可见,基于噪声驱动的方法能够有效地提高ND算法的学习能力。在后续的研究中,这种噪声驱动的学习模式被广泛扩展到不同的机器人应用中,包括运动学参数估计、循环运动控制和运动与力混合控制等。
基于噪声驱动的方法能够与ND算法结合,进而增强机器人系统的学习能力。然而,附加噪声\pmb{n} 会直接影响雅可比矩阵估计结果和控制信号,不利于机器人系统的稳定控制。
为了减轻噪声对机器人系统的负面影响,各种抗噪方法和滤波技术被研究并集成于机器人的学习与控制系统中。例如,卡尔曼滤波算法具有预测和估计能力,能够处理机器人的测量噪声和过程噪声,从而提高系统的精确性和稳定性。在文[63]中,一个自适应卡尔曼滤波器被设计以实现雅可比矩阵的估计过程。该方法提出了一个递归的线性系统状态估计方程,并通过测量关节角速度和末端执行器的数据对雅可比矩阵进行最优估计。其优势在于只需当前时刻的测量值和前一个采样周期的估计值即可进行雅可比矩阵估计,不需要大量的存储空间,非常适合计算机处理。因此,卡尔曼滤波算法与ND算法结合能够有效提高机器人学习与控制的稳定性和鲁棒性。
滑模控制是一种广为研究的非线性控制方法。其非线性表现为控制的不连续性,可以在机器人运动过程中根据系统的当前状态不断变化,迫使收敛系统按照预定的状态轨迹运动。滑模控制的优点是可以克服机器人系统的不确定性,对机器人学习问题具有鲁棒性。文[42]设计了多个自适应雅可比矩阵估计器来实现机器人雅可比矩阵学习和动力学与运动学参数估计。其核心原理在于构建自适应滑动矢量\pmb{s=\hat{J}\dot{\theta}-\dot p} ,并根据线性化公式和参数控制原理,设计多个全局收敛于滑动矢量的控制系统。在该系统下,机器人可以通过更新估计参数来跟踪期望轨迹。滑模控制的原理和ND算法的原理是类似的,因此滑模控制及其相关理论可以为ND方法提供可借鉴的改进方向。例如,文[66]借鉴滑模控制的设计公式改进了ZND算法,从而引入了有限时间收敛机制。
传感器系统是基于ND算法的机器人学习中不可缺少的一部分,能够提供机器人系统必要的数据以促进学习过程。传感器系统的精确程度直接影响基于ND算法的机器人学习性能。基于ND算法的机器人学习的文[26,55-66]均介绍了数据来源和相关传感器设备。作为最常见的传感器系统,末端深度相机能够获取物体、末端执行器等位置信息,进而实现机器人定位、姿态识别、运动检测等功能。一套精密而复杂的相机能够搭建动作捕捉系统。在该系统中,多个高速相机从不同角度对目标特征点进行跟踪,进而显著提高定位能力。此外,力(扭矩)传感器可以对机器人的受力情况进行监控,并根据数据分析,对机器人行为作出指导。编码器负责测量机器人的各个关节状态,并及时反馈机器人的运动状态;距离传感器能够基于光波或声波进行测距,有助于移动智能机器人的避障功能开发;声音传感器用于感受和捕捉在气体、液体或固体中的声波,进而实现语言识别。速度或加速度层的数据信息可以通过差分算法、滤波器等手段从位置层数据近似获得或通过特定的传感器进行测量。例如,物体的加速度可以通过惯性测量单元进行获取。
本节系统性地总结了ND算法及其相关技术。ND算法需要基于数据驱动技术实现参数学习,进而实现机器人系统的无模型控制。噪声驱动方法、卡尔曼滤波算法、滑模控制、传感器系统可以与ND方法结合进一步提升机器人系统的性能。与机器学习算法相比,其优势在于所需数据量小且不需要预训练。然而,实际机器人系统的实时性特征也对数据处理、噪声抑制、算法设计等多方面提出了更高的要求。
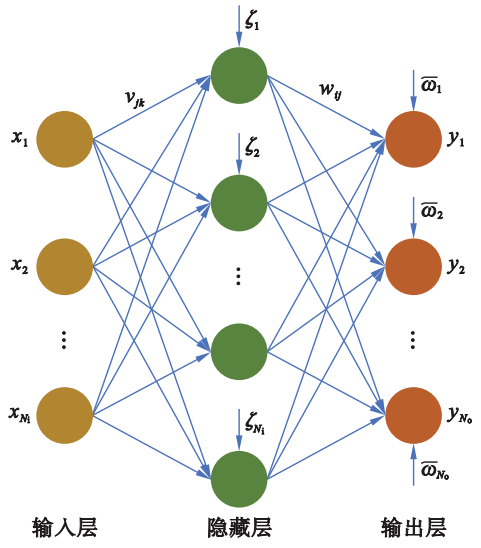
FNN方法是一种函数拟合方法。它能够通过简单非线性函数的多次复合,获得输入空间到输出空间的复杂映射关系。针对机器人系统的学习与控制问题,FNN方法被设计以实现机器人参数学习,进而弥补系统的不确定性。例如,反向传播(back propagation,BP)神经网络和径向基函数(radial ba-sis function,RBF)神经网络在一定条件下能够拟合任意连续曲线。它们能通过测量的机器人状态数据集,训练并更新权重参数,实现对机器人系统的参数估计。机器人逆运动学模型、正运动学模型、动力学模型和相关物理参数都可以成为FNN方法的拟合对象。如图3所示,FNN的结构包括输入层、隐藏层和输出层。其输出可以被表述为
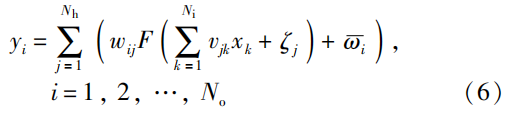
式中,\mathcal{x}_k 和y_i 分别表示神经网络的输入和输出;N_i 、N_h 和N_o 分别表示输入层、隐藏层和输出层的神经元数量;v_{jk} 和w_{ij} 分别表示隐藏层和输出层的权重;\zeta_j 和\bar{\omega}_i 分别表示隐藏层和输出层的偏置项;F(·) 表示隐藏层的激活函数,可以选择为sigmoid激活函数F(\chi)=1/(1+\text{exp}(-\chi)) 。进而,式(6)可以被简化为\pmb{y= A \bar{F}(P\bar{x})} ,式中,\pmb{A} \in \mathbb{R}^{N_o\times(N_h)+1} 和\pmb{P}\in \mathbb{R}^{N_h\times(N_i)+1} 表示两个增广权重矩阵;\pmb{\bar{x}}=[1,x_1,x_2,...,x_{N_i}]^T \in \mathbb{R}^{N_i+1} ;\pmb{y}=[y_1,y_2,...,y_{N_o}]^T \in \mathbb{R}^{N_o} ;
\pmb{\bar{F}}(\pmb{P\bar{x}})=[1,\pmb{F}(\pmb{P}^r_1\bar{\pmb{x}}),...,\pmb{F}(\pmb{P}^r_{N_h}\bar{\pmb{x}})]^T \in \mathbb{R}^{N_h+1} ,\pmb{P^r_i} 是矩阵P的第i 行。此外,\pmb{\bar{F}}(·) 可以看成从\mathbb{R}^{N_h}到\mathbb{R}^{N_h+1} 的映射。\zeta_j 和\bar{\omega}_i 分别构成矩阵\pmb{P} 和\pmb{A} 的第1列。基于上述结构,文[75]开发了一种基于FNN的学习方法以估计机器人动力学和执行器模型中的动力学参数并补偿系统的不确定性,实现了良好的无模型控制性能。文[75]在柔性机器人上测试了基于FNN方法和基于雅可比矩阵方法的两种逆运动学控制问题。其结果显示FNN方法不但能解决系统中的学习问题,而且具备响应速度快、控制精度高的特点。文[77]通过构建FNN结构以估计Baxter机器人的动力学参数,进而实现了同步避障和抓取任务。随着神经网络技术的发展,BP神经网络、RBF神经网络、极限学习机等多种FNN方法显著提升了机器人系统的学习能力。
BP神经网络能够学习并存储丰富的输入和输出映射关系,而不需要预先获得映射对应的数学方程。其学习原理采用最速下降法,通过反向传播不断调整网络的权值和偏差,实现网络误差最小化。其主要特征在于神经元数据是正向传播的,而误差是反向传播的。文[80]基于BP神经网络提出了一种简单且灵活的并联机器人标定方法,能够拟合校准参数与测量参数之间的关系,并提高了6自由度并联机器人的定位精度。文[81]提出了一种改进的BP神经网络以学习机器人的正运动学公式,进而解决逆运动学控制问题。
与BP神经网络相比,RBF神经网络在泛化能力、逼近精度和收敛速度方面具有优势。因此,RBF神经网络在机器人学习中能取得更高效的性能。具体而言,RBF神经网络中的径向基函数可以表示为
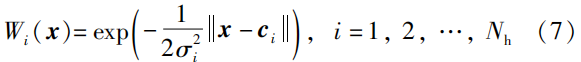
式中,x 为输入样本,c_i 是第i 中心点,\sigma_i 表示基函数第i 个标准差。式(7)构成了FNN的隐藏层空间。因此,其输入向量可以直接映射到隐藏层空间且无需权值连接。RBF神经网络的输出表示为
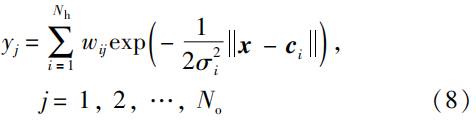
通过上述结构,从隐藏层空间到输出层空间的映射关系变为线性关系。换言之,RBF神经网络的输出是隐藏层元素的线性加权和。基于此,低维空间线性不可分的情况可以通过RBF转换成高维空间中线性可分的情况。该转换过程能够显著提升学习过程的收敛速度,同时避免局部极值问题。RBF神经网络在运动学和动力学系统的参数估计和系统辨识中有着重要的作用。在文[82]中,RBF神经网络被开发用于估计机器人的逆运动学关系,进而提高了机器人在无模型条件下的容错控制能力。该研究验证了RBF神经网络在实验中的性能优于BP神经网络。文[83]提出了一种分布式神经网络用于协同控制多机器人系统,并利用RBF神经网络估计逼近误差以补偿在通信带宽受限和时延存在下的系统不确定性。
其他FNN方法和相关的拓展研究给机器人学习与控制提供了有效的可行方案。极限学习机采用最小二乘法更新网络权值,在保证学习精度的前提下,其计算速度比传统学习算法更快。文[84]提出的基于极限学习机的方法能够利用数据进行实时学习以补偿机器人的动力学不确定性,进而实现末端执行器的触觉识别。此外,文[85]基于宽度学习思想,研究了无深度结构的增量学习系统。该方法能够通过增加神经节点以激发神经网络的收敛性与适应性,进而有效应用于微型机器人的伺服控制。
FNN方法已在机器人学习方面取得了一定的成功。作为总结,不同的FNN方法的比较见表2。为了获得满意的训练结果,一些结构复杂的FNN方法对数据和设备的要求很高。此外,FNN方法的学习过程可被理解为缺乏可解释性的黑箱,在一定程度上影响了学习结果的可信度。

RNN是一类具有短期记忆能力,能够用于处理和预测序列数据的神经网络。其神经元可以接受其他神经元的信息,也可以接受自身信息,进而形成具有环路的网络结构。如图4所示,RNN的隐藏层\pmb{h}_t 不仅取决于当前时刻的输入\pmb{x}_t ,还取决于上一时刻的隐藏层状态\pmb{h}_{t-1} 。这使得RNN方法可以有效地处理手写识别、语音识别等任务。RNN方法包括简单RNN、长短时间记忆网络、门循环单元、连续时间RNN和回声状态网络等。此外,RNN的方法在机器人控制方面有很多应用,例如一些文章,但很少涉及机器人学习。近年来,回声状态网络被应用于机器人学习中,并取得了良好的学习与控制效果。因此,在机器人学习方面,下文重点介绍回声状态网络。
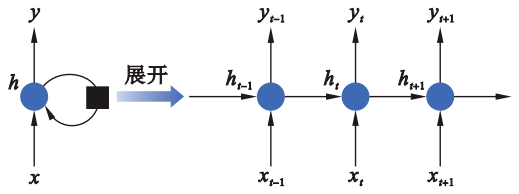
回声状态网络是一种特殊的RNN,具有一个稀疏连接的随机隐含层。该网络克服了基于梯度下降的学习算法所难以避免的收敛速度慢和易陷入局部极值等问题。在机器人学习与控制方面,文[91]利用回声状态网络建立了受小脑启发的预测模型,能够准确预测机器人在时序控制信号作用下的运动结果,并以此对原始控制信号进行准确调制。文[92]开发了基于回声状态网络的小脑启发的预测模型。该方法具体将任务空间误差转化为关节空间误差,并通过误差序列训练小脑预测模型,从而获得关节角度增量以实现机器人的高效控制。文[93]利用回声状态网络对机器人视觉系统的不确定性进行学习,进而实现机器人的视觉伺服控制。文[94]将回声状态网络应用于柔性机器人的物体跟踪任务中。该方法对时序因素的可控性强。
RNN方法能够在计算过程中体现过程动态特性,因此比FNN方法具有更强的动态计算能力。目前,结合RNN和机器人学习与控制技术的研究仍然不成熟,有待进一步开发。
基于神经网络的RL方法在机器人策略学习中发挥着至关重要的作用,能够解决机器人码垛、机械臂抓取、移动导航、自动驾驶等重要问题。图5展示了机器人强化学习的原理图。在机器人执行动作a_t 后,环境转换到新的状态s_{t+1} ,并提交奖励信号r_{t+1} 作为反馈。随后,机器人根据反馈执行新的动作a_{t+1} 。RL方法利用这种试错机制与环境进行交互,从而不断改善机器人策略。神经网络在强化学习系统中的作用在于拟合机器人交互过程中的动作分布。根据不同的原理,RL方法可以被划分为基于价值的RL、基于策略的RL和基于Actor-Critic框架的RL。
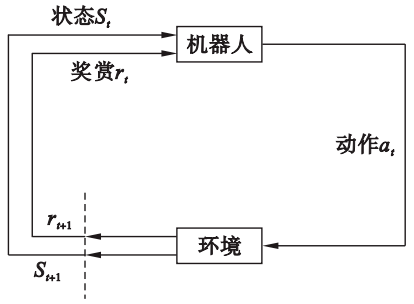
为了有效地评估策略\pi ,动作价值函数被设计为Q_{\pi}(s_t,a_t)=E(U_t|s_t,a_t) 式中E(·) 表示求均值操作。基于价值的RL的目标为获取最优动作值函数Q^*_{\pi}(s_t,a_t)=\text{max}_\pi Q_\pi(s_t,a_t) 。而后,通过最大化最优动作价值函数得到最优的动作策略a^*=\underset{a}{\operatorname{argmax}} Q^{*}\left(s_{t}, a_{t}\right) 以指导机器人系统进行决策。时序差分方法是常用的基于价值的RL方法,包括Sarsa方法和Q-learning方法。该方法能考虑少量状态和动作以更新动作值函数。多步时序差分方法是时序差分方法的改进算法,能同时处理多个奖励,从而获得更好的性能。当涉及大量或连续的状态或动作时,深度Q 网络(deep Q-network,DQN)被设计为Q(s_t,a_t;g) 以估计最优动作值函数Q^*(s_t,a_t) ,其中g 表示深度神经网络的参数。基于DQN,机器人被设定尝试各种与环境进行交互的动作,从而不断获得奖励。DQN的输入是状态s_t 和动作a_t ,而DQN的输出是评估动作的值。此外,该网络利用奖励r_t 训练参数g ,同时选择DQN的最大值所对应的动作为下一时刻的动作。经过足够的训练,DQN能够学习最优动作价值函数Q^*(s_t,a_t) ,间接获得最优策略。近年来,许多改进的框架和算法被开发出来,用以提高基于价值的RL方法的性能。美国人工智能企业DeepMind总结了DQN的6种主要改进方法,包括双DQN和基于竞争构架的DQN等,并提供了丰富的测试和比较结果。此后,文[99]提出了这些改进算法的深入分析和不同见解。在机器人技能学习方面,文[100]提出了基于双DQN网络的编队策略,能够控制多机器人系统接近目标并避免碰撞。文[101]提出了一种改进的DQN方法,能够实现多机器人系统的自主轨迹规划功能。文[102]将DQN开发为机器人逆运动学求解器,能够基于给定轨迹任务生成高自由度机械臂的关节空间轨迹。
基于策略的RL方法需要学习策略函数,进而利用学习的策略逼近状态价值函数V_\pi(s)=E_A(Q_\pi(s,A)) 。该方法需要将策略参数化,并通过策略网络\pi(a|s;\iota) 替代策略\pi(a|s) ,其中\iota 表示神经网络模型的参数。因此,状态值函数可以近似写成V(s;\iota)=\sum_a\pi(a|s;\iota)Q_\pi(s,a) 。V(s;\iota) 能够评价状态s 和策略网络\pi(a|s;\iota) 。在给定状态s 的情况下,状态值函数V(s;\iota) 的值越大,策略网络\pi(a|s;\iota) 越好。更新参数\iota 以提高状态值函数V(s;\iota) 是一种可行的策略优化方法。为了消除状态s 的随机性影响,目标函数被设计为O(\iota)=E_S(V(S;\iota)) 。由此,基于策略的RL的目标是通过更新参数\iota 以获得最大的O(\iota) 。策略梯度法是一种主流的参数更新方法,能够有效解决连续空间决策问题。该方法通过引入学习速率\zeta >0 和策略梯度以更新参数\iota ,具体更新公式为\iota\rightarrow\iota+\zeta·\partial V(s;\iota)/\partial\iota ,式中\partial V(s ; \iota) / \partial \iota=\sum_{a} \partial \pi(a \mid s ; \iota) / \partial \iota \cdot Q_{\pi}(s, a) 。然而,策略梯度法的缺点是策略估计结果存在较大方差。此外,该方法还存在样本利用率低、收敛速度慢的缺点。基于策略的RL方法在机器人学习与控制应用中获得了丰富的研究成果。文[106]开发一种改进的策略梯度算法,能够直接学习机器人的深度神经网络控制策略,不需要人工分析机器人控制模型。文[107]提出一种样本利用率高的RL算法,通过学习机器人的最佳运动参数以赋予机器人准确回击乒乓球的技能。
基于Actor-Critic框架的RL方法是一种同时学习动作价值函数和策略函数的前沿算法。该方法结合了价值网络Q(s_t,a_t;g) 和策略网络\pi(a|s;\iota) 以估计状态价值函数

因此,参数\iota 和参数g 的训练过程需要同步执行以提高系统动作评价的准确性并获得最优策略。Actor-Critic框架能够通过时序差分方法更新参数g ,并通过策略梯度方法更新参数ι。在训练过程中,策略网络\pi(a|s;\iota) 负责控制机器人运动,价值网络Q(s_t,a_t;g) 负责评估动作。基于Actor-Critic框架的RL方法的优势在于能够进行单步更新,且更新速度比基于策略的RL方法更快。然而,其缺点在于同时结合两个神经网络导致系统难以收敛。基于Actor-Critic框架的RL方法可应用于机器人在各种复杂环境中的最优阻抗控制,并保持一定的安全性。文[111]提出了一种基于Actor-Critic的RL方法并应用于机器人膝关节阻抗参数的自动调整,能够学习完整的膝关节运动学模型。文[112]提出了一种Actor-Critic高斯混合方法,该方法能够基于动态系统学习机器人技能,并通过与环境的相互作用将学习的技能调整于机器人的轨迹分布空间中。
基于RL方法的大部分研究都是在非真实物理环境中进行的。在真实机器人系统中,基于神经网络的RL方法仍然存在着难以解决的瓶颈问题。具体而言,RL方法需要机器人与现实环境之间丰富的交互数据。这要求机器人长时间执行各种交互动作,从而导致了昂贵的现实试错成本。为了解决这个问题,Sim2Real能够帮助现实机器人在模拟环境中使用数据进行学习,属于一种迁移学习方法。该技术在模拟环境中完成机器人控制策略的数据采集和网络训练过程,然后将获得的控制策略应用于实际的机器人。基于Sim2Real的RL技术被广泛应用于移动机器人、四足机器人、类人机器人等多种重要机器人的策略开发中。然而,模拟环境和现实环境之间存在不可避免的差异,会在一定程度上影响策略的执行效率。对此,神经增强仿真法和动态随机化处理法被提出以减小模拟环境和现实环境的差距,从而提高学习的可靠性。
综上所述,基于神经网络的RL方法是一种以目标为导向的学习方法。该方法通过不断与环境交互试错以获得足够的知识,从而使机器人能够做出合理的行为决策。其优势在于能够学习多变的环境模型,并解决无模型动态交互问题。然而,其缺点在于深度学习所需的昂贵数据成本和设备成本。此外,RL方法通常严重依赖于仿真,难以直接应用于实际机器人系统。
机器人学习与控制系统的正常运行依靠两个功能相异的内外循环。外循环管理系统的控制功能,而内循环主要负责系统的参数学习功能。从系统控制的角度来看,内部循环的收敛速度必须比外部循环更快,这对网络的参数设定给出特殊的限制。换言之,只有优越的学习能力才能保证机器人系统控制的精确性。这强调了面向不同功能性提升的机器人控制方案的重要性。为解决机器人的控制问题,传统方法通常会设计特定的优化方案来约束相关的性能指标,从而规划机器人的运动轨迹。常用的优化指标包括可操作性、关节漂移和动能消耗。基于模型学习的机器人控制方法将机器人优化方案表述为时变线性方程的数学求解问题。求解这些机器人优化方案的常用算法包括伪逆法、数值算法、神经网络法等。通常而言,机器人优化方案可以通过基于二次规划的统一框架整合目标函数和等式与不等式约束条件,从而得到泛化形式:
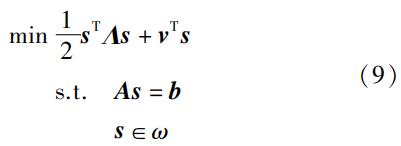
式中,\pmb{s} \in \mathbb{R}^n 表示机器人优化方案的决策变量,可以根据任务需求选择为关节速度、关节加速度、关节突加度、关节扭矩等;\Lambda \in \mathbb{R}^{n\times n} 表示一个正定的矩阵;\pmb{v}\in \mathbb{R}^n 表示待优化的指标,如复运动指标、可操作度优化指标和位置误差指标;\pmb{As=b} 表示根据任务要求设定的等式约束,可以选择为动力学约束等式、运动学约束等式、视觉约束等式等,其中 \pmb{A}\in \mathbb{R}^{c\times n} ,\pmb{b}\in \mathbb{R}^c ,\omega=\{\pmb{s}\in \mathbb{R}^n,\pmb{s}^-\le\pmb{s}\le\pmb{s}^+\} 表示决策变量的不等式约束集,其中\pmb{s}^- 和\pmb{s}^+ 分别表示决策变量的下限和上限。二次规划方案能够以统一的框架描述基于运动学模型、动力学模型、混合模型等的机器人控制方案。近年来相关的研究成果有效解决了避障规划、运动规划、可操作度优化、位置与力混合控制、视觉伺服等重要的机器人控制问题。基于模型的机器人控制方案中的学习问题可以通过结合ND方法和FNN方法的学习功能解决,从而构建机器人系统的同步学习与控制的统一框架。不同于工业机器人中使用的比例-积分-微分控制,方案更加注重于待优化的指标和不等式约束,更加具备功能性。此外,方案可以基于模型预测控制思想来构建,利用已有的模型、机器人系统当前的状态和未来的控制量以预测系统未来的输出。由于未来的控制量是未知的,模型预测控制需要设计误差函数进行辅助求解以得到有效的未来控制量序列。在每次控制周期结束后,机器人系统根据当前实际状态重新预测未来输出。ZHANG等提出了一种基于模型预测控制的二次规划方案,能够基于机器人运动学模型预测未来系统的输出行为,并通过求解最优控制问题将未来的跟踪误差最小化。文[128]将模型预测控制的思想融入机器人动力学控制中,有效考虑了关节扭矩的约束。不同于基于模型的机器人控制方案,基于学习的机器人控制方案需要实现参数学习并基于学习结果计算控制信号。
此外,方案可以通过二次规划求解器直接进行求解,从而得到方案的最优控制信号。需要说明的是,二次规划的求解器有很多,商业的求解器包括Gurobi、Cplex、Xpress和Mosek;免费求解器包括SCIP、CBC、GLPK和Matlab中的quadprog求解器等。与此同时,方案可以等价地转化为非线性方程组求解问题。因此,常用的二次规划求解器也包括处理非线性方程组求解问题的数值方法,例如94LVI(94 linear varia-tional inequality,LVI)算法、E47算法和M4法。
基于方案开发的机器人控制器通常拥有较高的求解速度以满足实时性要求。机器人控制问题的传统方法是伪逆法。基于该方法的控制器在驱动机器人实现给定任务的同时,能够优化单个额外目标。对于方案而言,基于伪逆法的控制器可以表述为
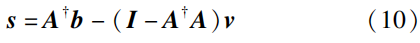
式中,\pmb{I}\in \mathbb{R}^{n\times n} 表示单位阵。虽然控制器结构简单且广泛应用于工业机器人控制中,但是它只能求解标准的单约束控制方案,无法处理涉及多个等式约束和不等式约束的复杂情况。这在一定程度上限制了伪逆法的应用范围。例如,以最小化关节速度无穷范数为目标的机器人控制方案就涉及多个不等式约束,无法通过基于伪逆法的控制器实现有效求解。
不同于基于伪逆法的控制器,基于ND方法的控制器凭借其强大的并行处理能力和计算能力在机器人学习与控制研究中取得了卓有成效的理论与实践成果。就其本质而言,ND方法属于一种ODE形式的实时求解算法,能够凭借全局指数收敛特性实现系统误差控制。因此,基于学习的机器人控制问题等价于求解ODE系统的平衡解问题。值得注意的是,所设计ODE系统可以直接基于任务要求与机器人模型构建动力学控制器,也可以基于方案的最优解问题构建线性方程组。后者可以通过Karush-Kuhn-Tucker条件获得,并满足线性方程组:

式中,\boldsymbol{H}=\left[\begin{array}{cc} \boldsymbol{A} & \boldsymbol{A}^{\mathrm{T}} \\ -\boldsymbol{A} & \mathbf{0} \end{array}\right] \in \mathbb{R}^{(c+n) \times(c+n)} ;\pmb{u}=\begin{bmatrix} s \\ \lambda \end{bmatrix}\in \mathbb{R}^{c+n} ,\pmb{\lambda}\in \mathbb{R}^c ,为等式约束的拉格朗日乘子;\pmb{r}=\begin{bmatrix} \pmb{-v} \\ \pmb{-b} \end{bmatrix} \in \mathbb{R}^{c+n} ;\pmb{u}\in \Omega ,\Omega=\{\pmb{u}\in \mathbb{R}^{c+n},\pmb{u}^-\le \pmb{u}\le \pmb{u}^+\} ,其中,\pmb{u}^+=\begin{bmatrix} \pmb{s} ^+\\ \pmb{h} \end{bmatrix} \in \mathbb{R}^{c+n} ,\pmb{u}^-=\begin{bmatrix} \pmb{s} ^-\\ -\pmb{h} \end{bmatrix} \in \mathbb{R}^{c+n} ,\pmb{h}\in \mathbb{R}^{c+n} 表示由极大的正数组成的向量。
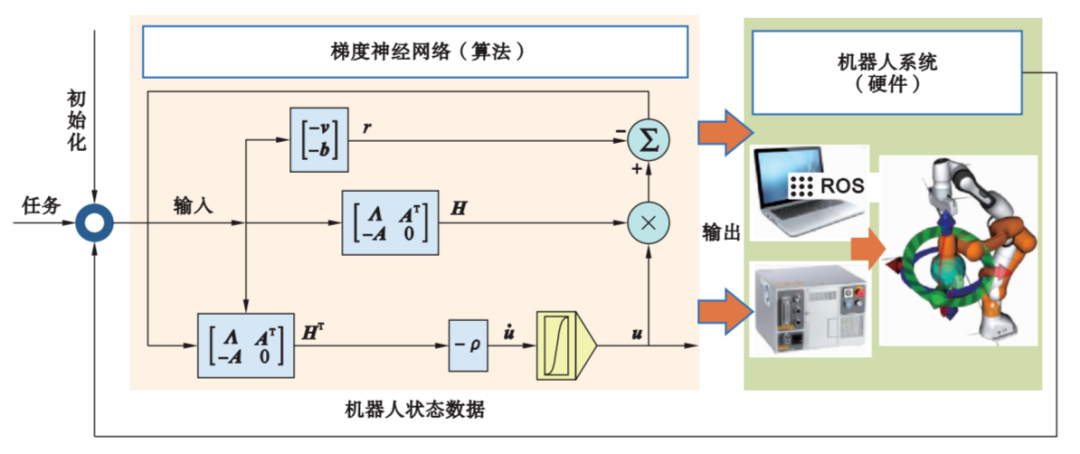
本节的后续内容将基于ND算法的控制器归纳为ZND控制器、梯度神经网络(gradient neural net-work,GNN)控制器和动态神经网络(dynamic neural network,DNN)控制器,并在下文中进行了详细介绍。以GNN控制器为例,其在机器人系统中的工作流程如图6所示。基于该网络结构,机器人系统的状态数据被测量作为反馈信息,进而驱动机器人实现给定任务。
ZND控制器能够将机器人时变最优化问题转化为时变等式求解问题,进一步归纳为零化问题进行求解。2002年,ZHANG等首次提出了一种基于神经动力学模型\pmb{\dot{\varepsilon}}=\pmb{-\mu\varepsilon} 的ZND控制器以在线求解线性方程组。以式(11)为例,ZND控制器将零化误差函数定义为\pmb{\varepsilon = Hu-r} ,并得到:
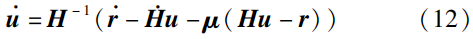
式中,\pmb{\mu}>0 为收敛参数;参数\pmb{\dot{u}} 、\pmb{\dot{r}} 、\pmb{\dot{H}} 分别为\pmb{{u}} 、\pmb{{r}} 、\pmb{{H}} 的时间导数;\pmb{{H}}^{-1} 表示矩阵\pmb{{H}} 的逆矩阵。式(12)的零化误差函数满足\pmb{{\varepsilon}}(t)=\pmb{{\varepsilon}}(0)\text{exp}(\pmb{{-\mu}}t) ,能够指数收敛于0,其收敛速度与\pmb{\mu} 成正相关。然而,式(12)无法处理关于决策变量的不等式约束条件。对此,文[132]提出了一种将不等式约束转化为等式约束的方式,进而赋予ZND控制器解决不等式约束的能力,在一定程度上拓展了ZND控制器在机器人学习与控制方面的求解能力。此外,后续改进的ZND控制器(如抗噪ZND、有限时间收敛ZND等)提高了系统的鲁棒性、收敛速度和容错能力。基于欧拉差分方法或其他多步差分法的离散ZND控制器能够顺利地嵌入机器人系统中。近年来,ZND控制器在机器人控制方面的拓展性研究包括重复运动控制、关节速度无穷范数最小化控制、多机器人协同控制等。此外,文[28]将ZND控制器和机器人学习算法相结合,实现了机器人系统无模型条件下的有效控制。然而,ZND控制器中涉及参数的导数项,可能由于外界噪声干扰而发生控制性能衰退的情况,这不利于机器人系统的长期运行。
GNN 控制器属于一种基于梯度下降法的实时 求解算法,能够利用梯度信息寻找目标函数最小化 的演化方向,并通过不断迭代调整机器人系统状态 以寻找最优解。对于式(11) 而言,GNN 控制器的 输出会驱使系统沿负梯度方向进行衍化,并收敛至 方案的最优解 。具体地,面向机器人控制问题的 GNN 控制器可以被推导为

式中,\rho >0 表示收敛系数,决定了机器人系统收敛速度和稳定状态的精度; ||·||^2 表示向量2范数的平方。GNN控制器的输出\dot{u} 决定了决策变量\pmb{u} 的变化方向,且\pmb{u} 的前n 个元素表示机器人的控制信号。文[142]证明了该控制器的收敛性,并验证了求解矩阵逆问题的可行性。然而,GNN控制器没有考虑动态参数的速度补偿,适合于求解静态问题。根据文[143]证明,对于动态问题而言,GNN控制器的误差函数\pmb{\varepsilon=Hu-r} 将收敛于非零的边界,进而增大了机器人系统的任务误差。对此,文[144]提出了一种自适应GNN控制器,通过开发自适应收敛系数提高计算精度和收敛速度,并在PUMA 560机器人上验证了该控制器的可行性。此后,文[56]对GNN控制器设计了速度补偿项,从理论上消除了机器人系统的滞后误差并通过投影函数施加了关节约束以确保机器人系统的安全性。文[145]中的研究工作将该控制器拓展至机器人的关节加速度控制中。此外,WEI等利用非线性互补函数将机器人系统中的不等式约束转变为等式约束,并引入误差积分项以有效提高机器人系统的抗噪能力。此后,文[146]提出了基于正交投影矩阵的GNN控制器,成功地解耦了机器人关节空间误差和位置误差,从而实现了更高的控制精度。上述研究表明,GNN控制器及其拓展方法的优势在于不涉及矩阵求逆计算且网络结构简单。
ZND控制器和GNN控制器在处理机器人不等式约束时,需要通过一定的转化技巧将不等式约束转化为等式约束并重新构造线性方程组进行求解。这个转化过程不但增加了控制器的搭建难度,而且增加了机器人系统的计算开销。针对这个问题,DNN控制器能够通过引入投影函数直接处理不等式约束,并且具备网络结构简单和计算复杂度低的优势。具体而言,一种基于线性变分不等式的原对偶神经网络(LVI-PDNN)在文[37]中被设计以求解线性方程组。作为一种特殊的DNN求解器,该方法提出了双桥理论,并将二次规划问题转化成了分段线性投影方程求解问题。具体地,面向机器人控制问题的LVI-PDNN被设计为
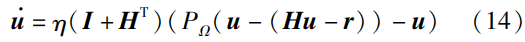
式中,\eta >0 表示收敛系数;投影函数P_{\Omega}(·) 是神经网络的有界激活函数,并被表述为
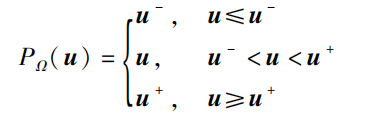
LVI-PDNN能够全局收敛于线性方程组的解,即机器人控制方案的最优解。类似于LVI-PDNN方法的离散数值算法包括94LVI算法和E47算法。这类方法被开发用于求解移动机器人视觉伺服、动力学系统控制等问题,并在仿真和实验中达到了毫米级的控制精度。
在后续的研究中,简化的DNN求解器被设计为
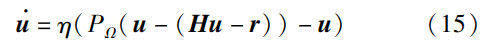
其控制框图如图7所示。文[150]证明了当矩阵\pmb{H} 连续可导且单调时,DNN(15)的解将全局收敛于\pmb{Hu=r} 的最优解。文[56]将简化的DNN控制器与基于梯度下降的学习算法结合在同一个方案中,从而实现了雅可比矩阵学习误差和机器人跟踪误差的同步收敛。基于类似的框架,一种用于求解多层变量约束方案的DNN控制器在文[151]中被研究。该求解器能够在缺乏机器人模型先验知识的条件下约束更深层决策变量。简言之,DNN控制器的优势在于能够直接处理不等式约束。此外,上述3种ND控制器的比较如表3所示。
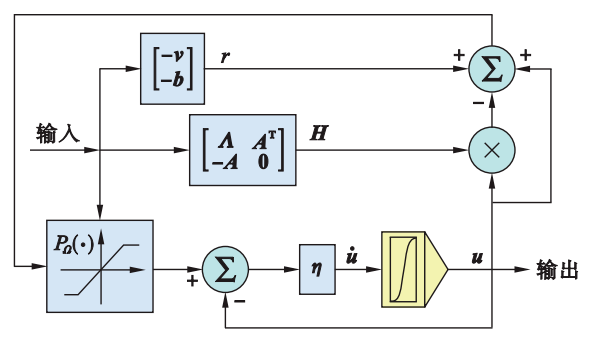

综上所述,基于ND方法的控制器有效提升了机器人系统的高效性、安全性和稳定性。目前,关于机器人控制器的抗噪性研究和交互研究仍然是机器人系统在实际应用中的重要问题。
ND方法、FNN方法、RNN方法和RL方法为解决机器人系统内部的学习与控制问题做出了巨大贡献,并取得了丰硕的理论与实践成果。然而,机器人还无法普及于人类社会中的各个领域中。其发展仍然存在许多问题与挑战。因此,本节将介绍机器人学习与控制领域的5个问题。
1) 数据问题:机器人学习算法依赖数据驱动技术进行学习或估计过程。这种学习过程要求获得机器人系统的状态数据,例如,Broyden算法需要获取末端执行器的实时速度信息。有限的传感设备条件会极大地限制机器人学习算法的可行性。另一方面,机器人系统的学习与控制精度也会受到传感器测量误差的影响。其次,传感器系统故障所导致的错误数据可能引发致命的事故。例如,2019年3月10日,埃塞俄比亚航空一架波音737 Max 8航班由于迎角探测器的错误数据在起飞6 min后坠毁。以上问题对高性能传感器、数据可信度、故障应对和数据处理方法提出了更高的要求。
2) 噪声问题:在实际机器人系统中,噪声是不可避免的,可能来源于测量、计算、环境等因素。现有的ND算法甚至会引入较小的附加噪声来促进学习过程。附加噪声能够增加系统输入的多样性,在一定程度上避免鞍点问题,进而提高收敛能力。然而,这一现象是缺乏可解释性的。此外,相对较小的附加噪声有利于学习过程的进行,但噪声本身也会影响机器人系统的控制精度。相关研究并没有分析和消除附加噪声对机器人系统的潜在影响。因此,提高基于噪声驱动的学习方法的可解释性和解决噪声对学习与控制系统的不利影响具备一定的研究意义。
3) 安全问题:机器人学习与控制系统的安全性体现在两个方面。一方面,用于控制机器人系统的算法需要是严格稳定的。在各种特殊情况下(如障碍物、时滞),其应保持稳定的全局收敛特性,这是保证机器人作业安全的前提。另一方面,基于神经网络的学习算法需要对外界环境的噪声干扰具有鲁棒性。机器人系统的实际执行环境是复杂多变且非结构化的,这会影响网络的输入数据。现有的神经网络技术鲁棒性还有待提高。当输入数据被污染后,其学习准确率会急剧下降。这必然会使机器人系统失控,并产生较大的控制误差,甚至损坏机器人。
4) 成本问题:作为机器人学习与控制技术的核心算法,神经网络在各种机器人应用场景中得到了广泛的应用。不同的实际场景也对神经网络的计算能力提出了多样化的要求。然而,复杂的深度神经网络拥有多隐藏层,在增强模型表达能力的同时也提高了其结构复杂度和数据需求量。因此,部分神经网络需要高性能的多核高速CPU和GPU进行复杂的单精度运算。对此,成本问题的重点是在不影响性能的前提下减少神经网络的计算量、数据需求和存储需求。因此,未来的研究方向需要开发更加高效、简洁的神经网络计算架构,进而降低硬件成本,提高数据利用效率。
5) 泛化问题:当遇到同类型的任务时,机器人需要有效利用所学习的知识来完成新任务,从而提高机器人系统的学习效率和灵活性。换言之,机器人需要根据原有的知识和技能适应新的环境和任务。然而,这方面的相关研究相对缺乏。因此,亟需提出增强机器人泛化性能的可行方案,进而提高机器人系统的智能化程度。
如前所述,当前机器人学习与控制研究仍面临着巨大挑战。这也表明机器人技术潜在的研究趋势。在未来,随着传感器技术、神经网络方法和数学理论的进步,机器人学习与控制系统将会变得更加智能、更加通用。同时,随着近年来软体机器人技术、脑机接口技术、自动驾驶技术、多机器人云服务技术等一系列新兴概念的成熟,机器人系统的服务性能也将趋于智能化和人性化。
近30年来,机器人系统借助ND方法、FNN方法、RNN方法和RL方法解决了学习与控制问题,并取得了丰富的理论与实践成果。然而,多方面尚存的挑战和问题仍然阻碍着机器人技术的进一步发展。在这样的研究背景下,本文对机器人学习与控制的研究主题进行了详细的回顾和讨论,综述了4种主要的神经网络技术。针对不确定性学习问题,重点介绍了ND方法、FNN方法、RNN方法和RL方法。这些方法能够完成模型学习任务或者动态决策任务。面向机器人控制问题,基于ND的控制器和数值方法凭借其全局指数收敛特性负责机器人系统的高效控制。最后,分析了基于神经网络的机器人学习与控制技术的5大挑战。笔者相信随着新兴技术的发展与成熟,未来机器人会变得更加高效、智能且易于沟通,更具安全性、稳定性和通用性。