在应用计量经济分析中，有两个基础且重要问题需要关注：

1. 改变因变量和（或）自变量的测度单位（the units of measurement）对OLS估计量将产生什么样的影响？
2. 如何在回归分析中纳入常见的函数形式，以及函数形式变化对回归结果的解释有何影响？

本篇文档是对第一个问题的解答，数据处理和分析结果在Stata中完成。对第二个问题的回答将在下一篇文档中展开，旨在通过两篇精简的技术短文，对上述两个关键问题做出深入浅出的回答。

1. 变量测度单位变换对结果解读的影响

执行回归命令前，明确变量的单位至关重要。下式为一个简单的企业CEO工资决定方程，salary 是以1000元为单位的CEO年度工资水平，roe为CEO所在公司前三年的平均资本权益报酬率（return on equity），由净收入占共同权益的比重定义，例如，roe=10表示平均资本权益报酬率为10%。

salary = \beta_0 + \beta_1\cdot roe + u

此时，斜率（slope）\beta_1 测度了当公司roe增加1个单位时以1000元为单位的年度工资的变化数量。表1展示了一个示例数据的变量描述性统计结果。其中，salary的均值为1281.12，单位为1000元，即1990年平均年收入为128.112万元；salardol为1元为单位的工资水平（salardol = salary × 1000）。roe为由单个观测值1988、1989和1990三年的平均值计算而得，样本均值约为17.18%（注意：这里没有用十分位数进行表示，如0.1718，而是用%表示）；同理，由于roe的单位为1%，可令roedec=roe/100，即调整后的单位为0.01。

 use "http://fmwww.bc.edu/ec-p/data/wooldridge/ceosal1.dta", clear //示例数据来自Wooldridge的教材
 gen salardol= 1000*salary
 gen roedec=roe/100
 describe
 summarize //表1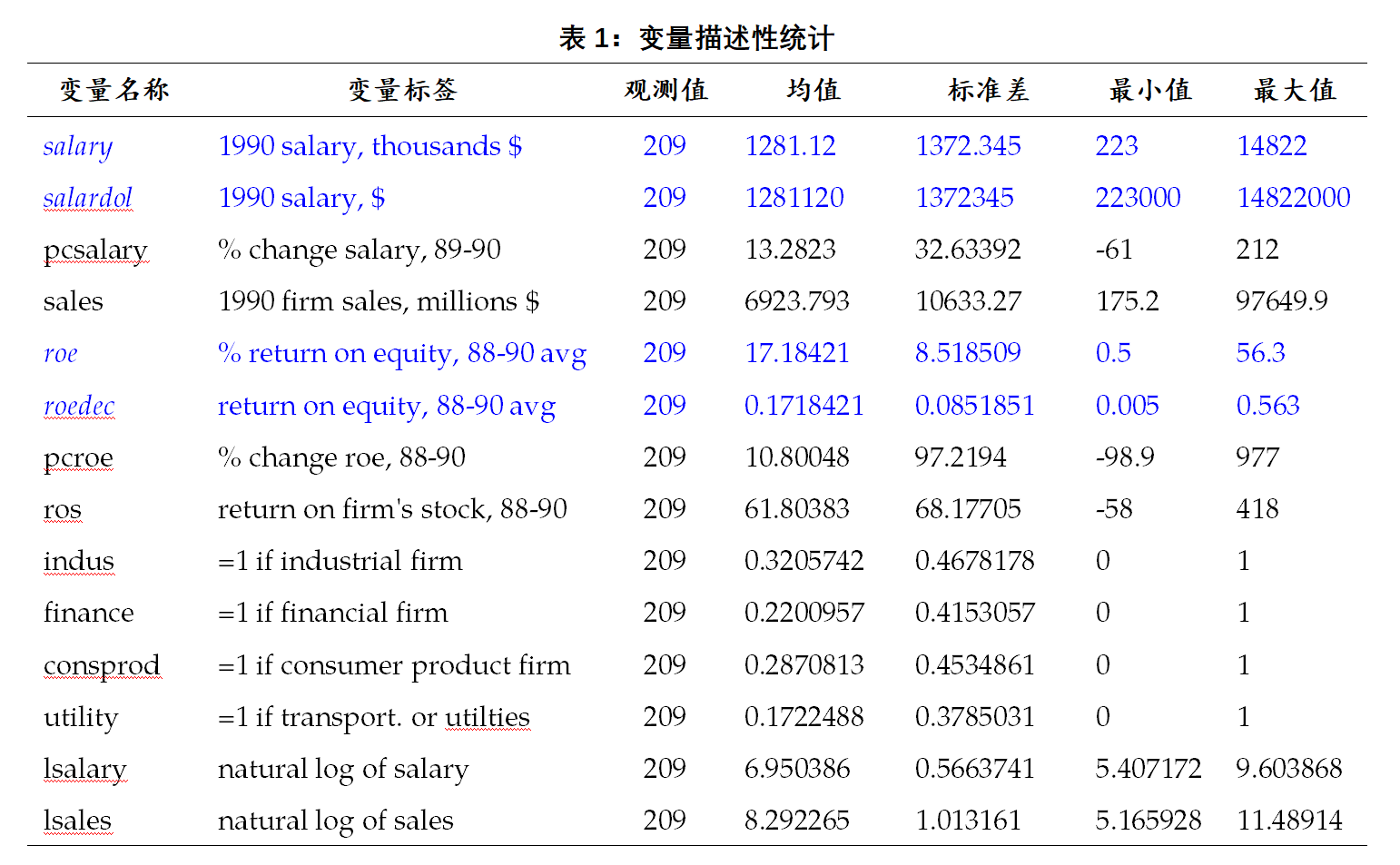

复制

2. 因变量测度单位成倍变化的影响

表2中的模型（1）和模型（2）分别展示了不同收入测量单位下的回归结果，可得样本回归函数（sample regression function）或OLS回归直线（OLS regression line）如下：

模型（1）： \hat {salary} = 963.2+18.5\cdot roe \\ 模型（2）：\hat {salarydol} = 963191.3+18501.2\cdot roe

由上可知，不论是截距项还是斜率项，对回归结果的解释不因工资水平（因变量）测度单位的不同而存在实质性差异。解释方式的差异仅在于salary的单位含义上。更一般地，若因变量按照乘以c倍变化（c≠0）（本例为c=1000），则回归的结截距项和斜率项也同样乘以c倍（本例为c=1000）。

*表2模型（1）
 reg salary roe    //salary in 1000 $
 est store m1

*表2模型（2）
 reg salardol roe  //salary in 1 $
 est store m2

*表2
 esttab m1 m2 using lec05.rtf, mtitles("工资(in $1000)" "工资(in $1)")  ///
    						   title(表：工资回归结果)                   ///
                               se scalars(N r2_a)                      ///
                               star(* 0.10 ** 0.05 *** 0.01) replace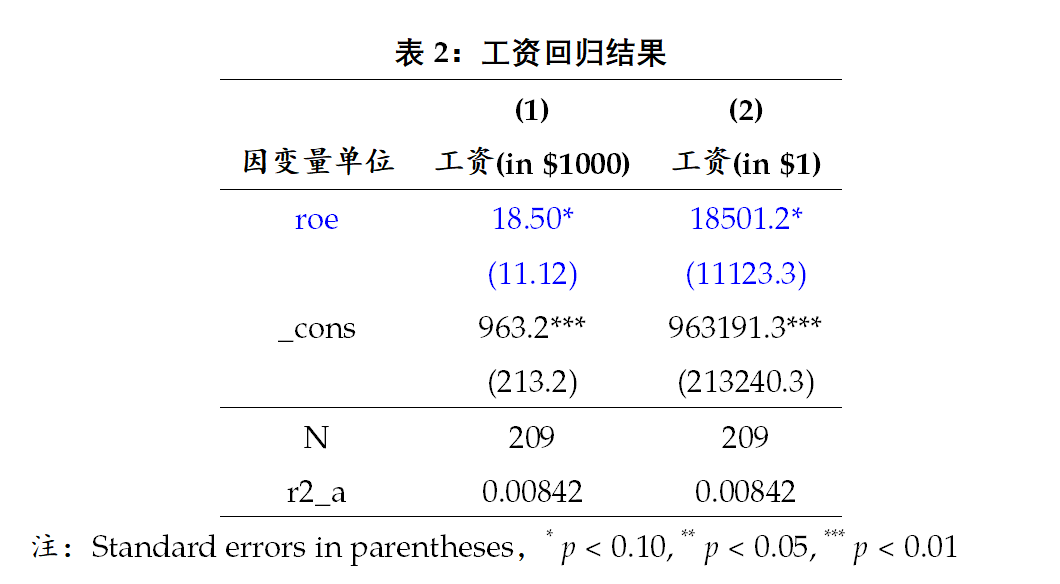        

复制

3. 自变量测度单位成倍变化的影响

表3中的模型（1）和模型（2）分别展示了不同经营收益测量单位下的回归结果，可得样本回归函数（sample regression function）或OLS回归直线（OLS regression line）如下：

模型（1）： \hat {salary} = 963.2+18.5\cdot roe \\ 模型（2）：\hat {salary} = 963.2+1850.1\cdot roe dec

由上可知，不论是截距项还是斜率项，对回归结果的解释不因经营收益（自变量）测度单位的不同而存在实质性差异。解释方式的差异仅在于roe的“变化1个单位”的含义上。更一般地，若自变量按照乘以c倍变化（c≠0）（本例为c=1/100），则回归的结截距项不变，仅斜率项乘以1/c倍（本例为1/c=100）。截距项不变也很好理解， 因为当roedec=0或roe=0时，对相同测度单位的工资而言，其期望值当然是相等的。

*表3模型（1）
 reg salary roe     //roe in 1%
 est store m3

*表3模型（2）
 reg salary roedec  //roe in 1/100
 est store m4
 
*表3
sttab m3 m4 using lec05.rtf, mtitles("业绩(in 1%)" "业绩(in 0.01)" ）  ///
    						 title(表：工资回归结果)                   ///
                             se scalars(N r2_a)                      ///
                             star(* 0.10 ** 0.05 *** 0.01) replace        

复制

此外，表2和表3的回归结果还表明，OLS回归的拟合效果（goodness-of-fit）不依赖于因变量或是自变量测度单位的变化而改变。上述结果还缺少因变量单位为 $1、自变量单位为0.01时的回归结果。为此，表4展示了所有可能的组合。

*表4模型（1）
 reg salary roe         //roe in  1%
 est store m3
 
*表4模型（2）
 reg salary roedec      //roe in 1/100
 est store m4
 
*表4模型（3）
 reg salardol roe     //roe in  1%
 est store m5

*表4模型（4）
 reg salardol roedec  //roe in  1%
 est store m6

 esttab m3 m4 m5 m6 using lec05.rtf, mtitles("业绩(in 1%)" "业绩(in 0.01)" "业绩(in 1%)" "业绩(in 0.01)")  ///
    								 title(表：工资回归结果)                      ///
                                     se scalars(N r2_a)                         ///
                                     star(* 0.10 ** 0.05 *** 0.01) replace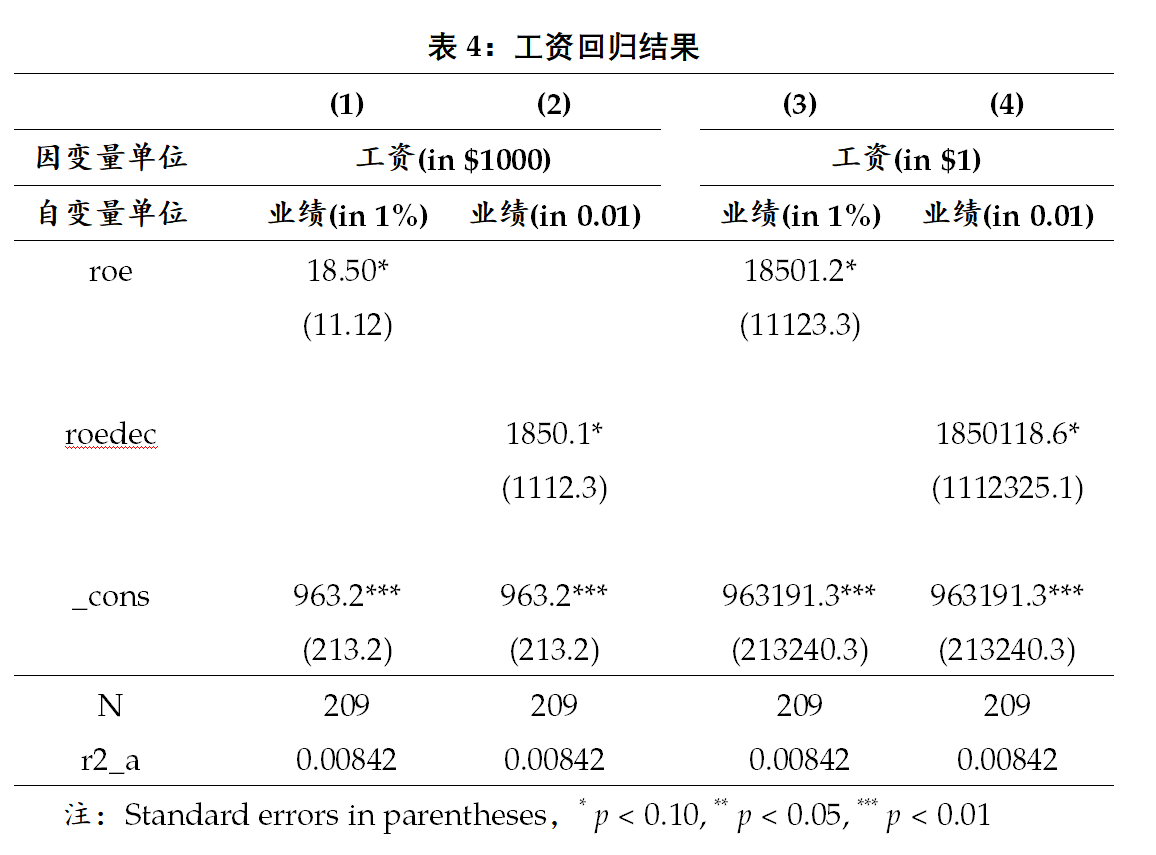        

复制

- - - - - - - - - -

版本记录

第一版：2023-02-06 （初稿）