所属分类:web前端开发

前端(vue)入门到精通课程:进入学习
Apipost = Postman + Swagger + Mock + Jmeter 超好用的API调试工具:点击使用
React中的Fiber任务都应该知道吧,而且不同的Fiber任务有不同的优先级,React需要先处理优先级高的任务。例如,用户的点击和输入,这些都是高优先级的任务,因为用户的操作肯定希望马上就会有效果,这样才能提升用户体验。而比如animation事件的优先级肯定要低一点。新进来的高优先级任务进去队列后,React需要优先处理。【相关推荐:Redis视频教程】
为了存储这些任务,React中有两个任务池。
// Tasks are stored on a min heap
var taskQueue = [];
var timerQueue = [];
登录后复制taskQueue与timerQueue都是数组,前者存储的是立即要执行的任务,而后者存的则是可以延迟执行的任务。
var newTask = {
id: taskIdCounter++, // 标记任务id
callback, // 回调函数
priorityLevel, // 任务优先级
startTime, // 任务开始时间,时间点
expirationTime, // 过期时间,时间点
sortIndex: -1, // 任务排序,取值来自过期时间,因此值越小,优先级越高
};登录后复制React中一旦来了新任务,就会先用currentTime记录当前时间(performance.now()或者Date.now()),如果任务有delay参数,那么任务开始执行时间startTime = currentTime + delay;。接下来通过startTime > currentTime如果成立,证明任务是可以延期的,那么任务进入timerQueue,否则进入taskQueue。
React怎么找到优先级最高的任务呢,以taskQueue为例,它是动态的任务池(任务队列),数据形式上就是一个数组。当然可以根据优先级进行排序,也就是Array.sort,当有新任务入队后,先排序,然后找出优先级最高的任务执行。但是Array.sort的平均时间复杂度是O(nlogn),并不是最好的解决方案。
taskQueue的newTask中排序用的是sortIndex,这个值取自过期时间expirationTime,也就意味着优先级越高的任务越需要理解执行,那么过期时间就越小,也就是说,优先级越高,过期时间就越小,sortIndex自然就越小。其实,这就是一种优先队列。
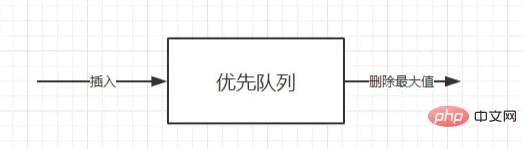
优先队列也是一种队列(首先它是一个队列,其次是尾进头出),只不过不同的是,优先队列的出队顺序是按照优先级来的;在有些情况下,可能需要找到元素集合中的最小或者最大元素,可以利用优先队列ADT来完成操作,优先队列ADT是一种数据结构,它支持插入和删除最小值操作(返回并删除最小元素)或删除最大值操作(返回并删除最大元素)。
如果最小键值元素拥有最高的优先级,那么这种优先队列叫做,升序优先队列(即总是先删除最小的元素)。类似的,如果最大键值元素拥有最高的优先级,那么这种优先队列叫作降序优先队列(即总是先删除最大的元素);由于这两种类型时对称的,所以只需要关注其中一种,如升序优先队列。
例如:买车票的时候,我们都在排队,优先级是一样的,谁在队伍前面,谁就先买票,但是这时候来了个军人,他的优先级高,直接就排在了队伍的最前面。
在React中用最小堆(小根堆,小顶堆。。。)来实现这种功能。就是把taskQueue变成最小堆,然后取出对顶任务执行,对taskQueue堆化,维持它依然是一个最小堆的数据结构。往taskQueue插入新任务的时候,也要进行堆化,始终保持它是一个最小堆。
有些地方称堆为优先队列(不准确),首先它是队列,有队列的特性,也就是“先进先出”。其次这个队列中的元素是有优先级的,优先级高的会排在前面。
准确来说,堆是实现优先队列的一种方式。当然优先队列还可以用其他方式来实现。
之前我们说过堆排序是不稳定排序,但taskQueue希望这个过程是稳定的,也就是说,如果有可能两个任务的过期时间一样,那这个时候就要看谁先进入的任务池了,也就是newTask的id的值,每次来了新任务,id都会加1。
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
}登录后复制在了解最小堆之前,先来温习一下基础知识。
是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
从图形形态上看,满二叉树外观上是一个三角形。
如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
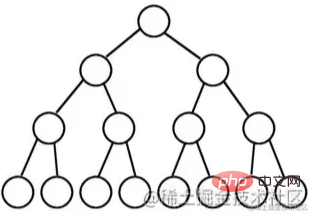
满二叉树,是“女儿双全”,非常圆满,所以叫满二叉树。
除去叶子节点, 所有节点的度都是 2。也就是说,所有的节点的度只能是0或2。
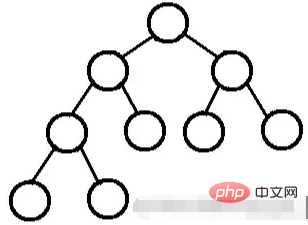
完美二叉树,要么没有孩子,要么儿女双全。
满二叉树的英文原文:
A Full Binary Tree (FBT) is a tree in which every node other than the leaves has two children.
完美二叉树的英文原文:
A Perfect Binary Tree(PBT) is a tree with all leaf nodes at the same depth. All internal nodes have degree 2.
国外的所有书籍参考的是最早翻译的关于满二叉树,和完美二叉树的教材,但是最早翻译的文章翻译错了。现在国内的话,我们只能将错就错了(所有人都错,那错的也就是对的了。比如说客。。。)。如果要和外国友人讨论这两个概念,就要注意了哦。
A Complete Binary Tree (CBT) is a binary tree in which every level,except possibly the last, is completely filled, and all nodes are as far left as possible.
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
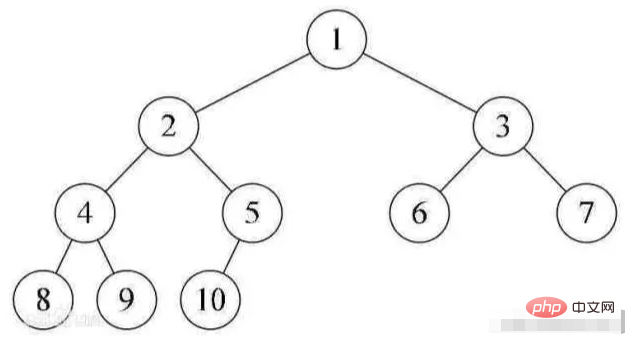
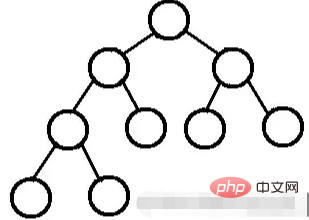
堆是一棵完全二叉树。
堆总是满足下列性质:
还要先认识下大根堆和小根堆,完全二叉树中所有节点均大于(或小于)它的孩子节点,所以这里就分为两种情况,最大堆和最小堆。
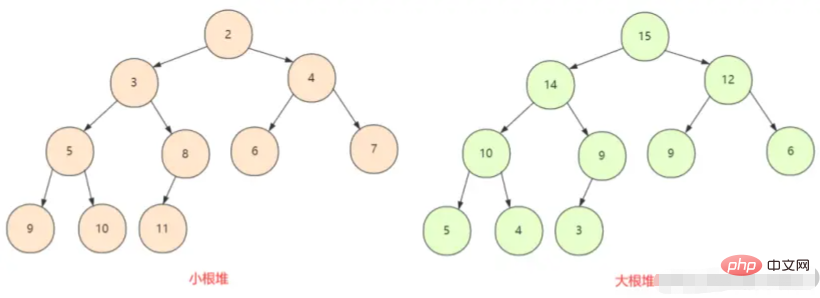
堆通常是一个可以被看做一棵 完全二叉树 的数组对象。 当然,二叉树也可以用数组表示。
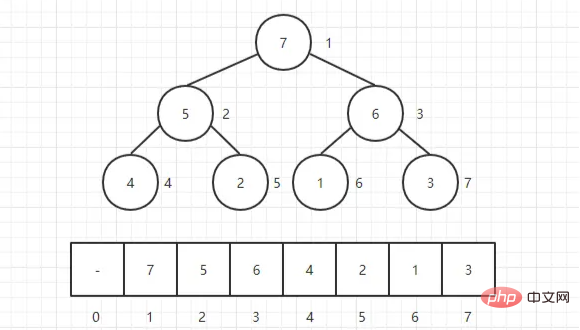
核心思想是,先建堆,后调整。
对于二叉树(数组表示),我们从下往上进行调整,从**「第一个非叶子节点」**开始向前调整,对于调整的规则如下:
建堆是一个O(n)的时间复杂度过程。
①从第一个非叶子节点开始判断交换下移(shiftDown),使得当前节点和子孩子能够保持堆的性质
②但是普通节点替换可能没问题,对如果交换打破子孩子堆结构性质,那么就要重新下移(shiftDown)被交换的节点一直到停止。
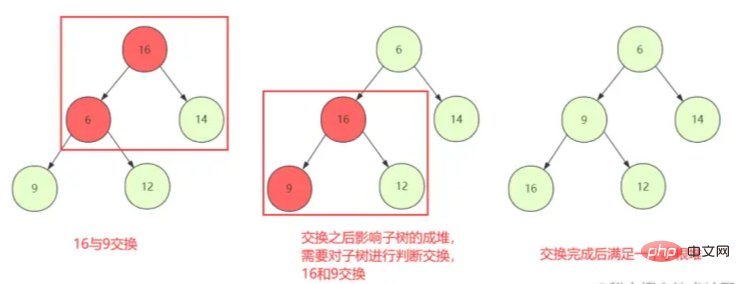
堆构造完成,取第一个堆顶元素为最小(最大),剩下左右孩子依然满足堆的性值,但是缺个堆顶元素,如果给孩子调上来,可能会调动太多并且可能破坏堆结构。
① 所以索性把最后一个元素放到第一位。这样只需要判断交换下移(shiftDown),不过需要注意此时整个堆的大小已经发生了变化,我们在逻辑上不会使用被抛弃的位置,所以在设计函数的时候需要附带一个堆大小的参数。
② 重复以上操作,一直堆中所有元素都被取得停止。
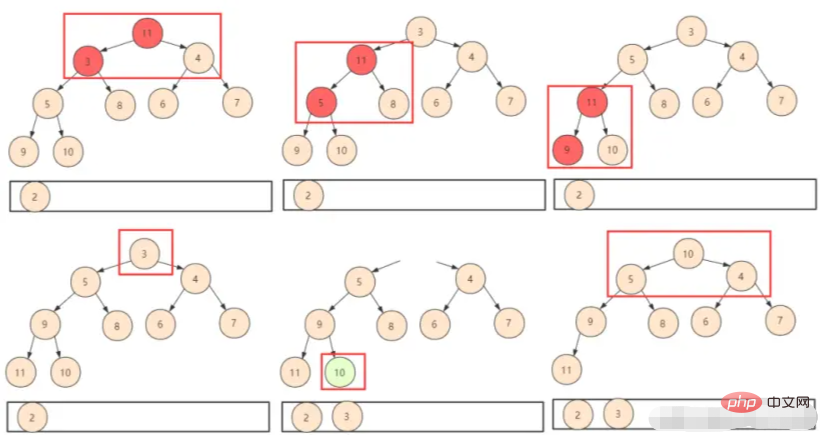
而堆算法复杂度的分析上,之前建堆时间复杂度是O(n)。而每次删除堆顶然后需要向下交换,每个个数为logn个。这样复杂度就为O(nlogn),总的时间复杂度为O(n)+O(nlogn)=O(nlogn)。
堆适合维护集合的最值。
堆pop出一个元素后,再次调整获取堆顶元素(也就是第二个最值)的花销比较低,因为pop出元素后,堆是一个半成品,在一个半成品上获取第二个最值的cost当然比较低,时间复杂度为O(logn),但如果遍历一遍找到第二个最值的话,时间复杂度为O(n)。
代码采用Javascript ES6的写法。
class Heap {
constructor(data, comp) {
this.data = data ? data : [];
// 比较规则:更加灵活,可以比较数值,也可以比较对象
this.compartor = comp ? comp : (a-b) => a-b;
// 调整为堆(优先队列)
this.heapify();
}
heapify() {
if(this.size() <= 1) return;
// 从第一个非叶子节点开始调整,也可以从最后一个元素开始调整
for(let i=Math.floor((this.size()-2)/2); i>=0; i--) {
// 调整堆, 向下调整也可以用递归来实现,这里用迭代来实现
this.shiftDown(i);
}
}
// 向下调整
shiftDown(i) {
let left = 2*i +1;
let right = 2*i +2;
let len = this.size();
while(i < len) {
let findIndex = i;
// 左孩子更“大”
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = left;
}
// 右孩子更“大”
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = right;
}
if(i !== findIndex) {
// 当前节点和更“大”的值进行交换
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// 调整完本层,可能会影响下层的堆的特性,所以要继续调整下层(迭代实现,也可以递归)
i = findIndex;
left = 2*i +1;
right = 2*i +2;
}
else {
// 如果无需调整,则跳出(必须跳出,否则循环无法结束)
break;
}
}
}
// 向上调整
shiftUp(i){
// 找到parent的下标
let parentIndex = Math.floor((i-1)/2);
// 最高调整到0
while(parentIndex >=0 ) {
let findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
if(findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = findIndex;
parentIndex = Math.floor((i-1)/2);
}
else {
break;
}
}
}
// 获取堆中所有元素的个数
size(){
return this.data.length;
}
// 获取堆首部元素
peek(){
if(!this.size()) return null;
return this.data[0];
}
// 往堆中添加一个元素
push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// 从堆里弹出堆首元素
pop(){
if(!this.size()) return null;
let res = this.data[0];
if(this.size() == 1) {
this.data.pop();
}
else {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
this.shiftDown(0);
}
return res;
}
}登录后复制 let arr = [2,9,8,6,3,10,5,7,4,1];
let comp = (a, b) => a-b;
let heap = new Heap(arr, comp);
let res = [];
while(heap.size()) {
res.push(heap.pop());
}
console.log(res);登录后复制arr里的元素也可以是一个对象。
React源码中的目录packages/scheduler,就是React的任务调度模块相关的代码。
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. and its affiliates.
*
* This source code is licensed under the MIT license found in the
* LICENSE file in the root directory of this source tree.
*
* @flow strict
*/
type Heap = Array<Node>;
type Node = {|
id: number,
sortIndex: number,
|};
export function push(heap: Heap, node: Node): void {
const index = heap.length;
heap.push(node);
siftUp(heap, node, index);
}
export function peek(heap: Heap): Node | null {
const first = heap[0];
return first === undefined ? null : first;
}
export function pop(heap: Heap): Node | null {
const first = heap[0];
if (first !== undefined) {
const last = heap.pop();
if (last !== first) {
heap[0] = last;
siftDown(heap, last, 0);
}
return first;
} else {
return null;
}
}
function siftUp(heap, node, i) {
let index = i;
while (true) {
const parentIndex = (index - 1) >>> 1;
const parent = heap[parentIndex];
if (parent !== undefined && compare(parent, node) > 0) {
// The parent is larger. Swap positions.
heap[parentIndex] = node;
heap[index] = parent;
index = parentIndex;
} else {
// The parent is smaller. Exit.
return;
}
}
}
function siftDown(heap, node, i) {
let index = i;
const length = heap.length;
while (index < length) {
const leftIndex = (index + 1) * 2 - 1;
const left = heap[leftIndex];
const rightIndex = leftIndex + 1;
const right = heap[rightIndex];
// If the left or right node is smaller, swap with the smaller of those.
if (left !== undefined && compare(left, node) < 0) {
if (right !== undefined && compare(right, left) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
heap[index] = left;
heap[leftIndex] = node;
index = leftIndex;
}
} else if (right !== undefined && compare(right, node) < 0) {
heap[index] = right;
heap[rightIndex] = node;
index = rightIndex;
} else {
// Neither child is smaller. Exit.
return;
}
}
}
function compare(a, b) {
// Compare sort index first, then task id.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ? diff : a.id - b.id;
}登录后复制我们自己实现的最小堆和React中的实现略有不同,但是思路是一样的,只是代码写法不同而已。
React中的任务调度是用最小堆来实现的,如果我们之前就对最小堆有一定了解,那在学习这块内容的时候就会更快一点。个人认为,前期知识积累是多么重要啊,但是这个过程可能会比较枯燥。 这个时候,是不是觉得自己也会一些算法了,其实这些算法是入门级别的,甚至还没有入门。因为在React的任务调度场景中,要实现的需求是非常明确的,而且要采用什么样的数据结构和算法也是明确的。在实际的一些场景中,我们知道了具体的需求,但是并不知道用什么数据结果和算法,就需要把需求抽象一下,根据抽象的数据模型来设计具体的数据结构和算法,这些才是重点。
更多编程相关知识,请访问:编程视频!!
以上就是深入了解React中的任务调度算法的详细内容,更多请关注zzsucai.com其它相关文章!
