回答网络系统的价值跟用户数量的关系是什么

其价值跟用户数量的平方成正比；网络使用者越多，价值就越大。梅特卡夫定律认为：一个网络的价值等于该网络内的节点数的平方，而且该网络的价值与联网的用户数的平方成正比；也就是说，一个网络的用户数目越多，那么整个网络和该网络内的每台计算机的价值也就越大，表现为网络经济的高渗透率。

php入门到就业线上直播课：进入学习
API 文档、设计、调试、自动化测试一体化协作工具：点击使用

本教程操作环境：windows7系统、Dell G3电脑。

网络系统的价值跟用户数量的平方成正比。

梅特卡夫定律认为，一个网络的价值等于该网络内的节点数的平方，而且该网络的价值与联网的用户数的平方成正比。

梅特卡夫定律（网络技术发展规律）

梅特卡夫定律（英语：Metcalfe's law）是一个关于网络的价值和网络技术的发展的定律，由乔治·吉尔德于1993年提出，但以计算机网络先驱、3Com公司的创始人罗伯特·梅特卡夫的姓氏命名，以表彰他在以太网上的贡献。其内容是：一个网络的价值等于该网络内的节点数的平方，而且该网络的价值与联网的用户数的平方成正比。

该定律指出，一个网络的用户数目越多，那么整个网络和该网络内的每台计算机的价值也就越大，表现为网络经济的高渗透率。

定律表示：

网络价值与用户数的平方成正比。网络使用者越多，价值就越大。换句话说，某种网络，比如电话的价值随着使用用户数量的增加而增加。现在如日中天的电子商务网站eBay就是最好的例证。

即网络的价值 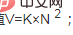；（K为价值系数，N为用户数量。）

网络的价值与网络规模的平方成正比。具体表现是网络价值与网络节点数的平方，与联网用户的数量的平方成正比。

背后理论

梅特卡夫定律背后的理论，亦即所谓网络的外部性效果(Network Externalty)：使用者愈多对原来的使用者而言，不仅其效果不会如一般经济财产（人愈多分享愈少），反而其效用会愈大。大体而言，摩尔定律加上产业合流现象形成到处信息化，梅特卡夫定律再把到处信息化的企业，以网络外部性的乘数效果加以连结，终于造就一个规模可与实体世界相媲美，充满了无数商机及成长潜力惊人的全球化电子商务市场。

意义：

梅特卡夫法则是基于每一个新上网的用户都因为别人的联网而获得了更多的信息交流机会，指出了网络具有极强的外部性和正反馈性：联网的用户越多，网络的价值越大，联网的需求也就越大。这样，我们可以看出梅特卡夫定律指出了从总体上看消费方面存在效用递增，即需求创造了新的需求。

应用价值

有的博客的门户网站根据这条定律计算它的价值，并以此作为计算博客参与该门户网站获得股权的测算依据。

梅特卡夫定律是一条关于网上资源的定律，该定律由新科技推广的速度决定，所以网络上联网的计算机越多，每台电脑的价值就越大。新技术只有在有许多人使用它时才会变得有价值。使用网络的人越多，这些产品才变得越有价值，因而越能吸引更多的人来使用，最终提高整个网络的总价值。一部电话没有任何价值，几部电话的价值也非常有限，成千上万部电话组成的通讯网络才把通讯技术的价值极大化了。当一项技术已建立必要的用户规模，它的价值将会呈爆炸性增长。一项技术多快才能达到必要的用户规模，这取决于用户进入网络的代价，代价越低，达到必要用户规模的速度也越快。有趣的是，一旦形成必要用户规模，新技术开发者在理论上可以提高对用户的价格，因为这项技术的应用价值比以前增加了。进而衍生为某项商业产品的价值随使用人数而增加的定律。

信息资源的奇特性不仅在于他可以被无损耗的消费，如一部古书从古至今都在“被消费”，但不可能“被消费掉”，而且信息的消费过程很可能同时就是信息的生产过程，它所包含的知识或感受在消费者那里催生出更多的知识或感受，消费它的人越多，它所包含的资源总量就越大。互联网的威力不仅在于它能使信息的消费者数量增加到最大限度（全人类），更在于它是一种传播与反馈同时进行的交互性媒介（这是它与报纸、收音机和电视机最不一样的地方）。

所以梅特卡夫断定，随着上网人数的增长，网上资源将呈几何级数增长。

更多相关知识，请访问常见问题栏目！

以上就是网络系统的价值跟用户数量的关系是什么的详细内容，更多请关注zzsucai.com其它相关文章！