python教程：一起来分析Python队列相关应用与习题

程序员必备接口测试调试工具：立即使用
Apipost = Postman + Swagger + Mock + Jmeter
Api设计、调试、文档、自动化测试工具
后端、前端、测试，同时在线协作，内容实时同步

推荐学习：python教程

0. 学习目标

我们已经学习了队列的相关概念以及其实现，同时也了解了队列在实际问题中的广泛应用，本节的主要目的是通过队列的相关习题来进一步加深对队列的理解，同时能够利用队列降低一些复杂问题解决方案的时间复杂度。

1. 使用两个栈实现一个队列

[问题] 给定两个栈，仅使用栈的基本操作实现一个队列。

[思路] 解决此问题的关键在于栈的反转特性，入栈的一系列元素在出栈时会以相反的顺序返回。因此，使用两个栈就可以实现元素以相同的顺序返回(反转的元素序列再次反转后就会得到原始顺序)。具体操作如下图所示：

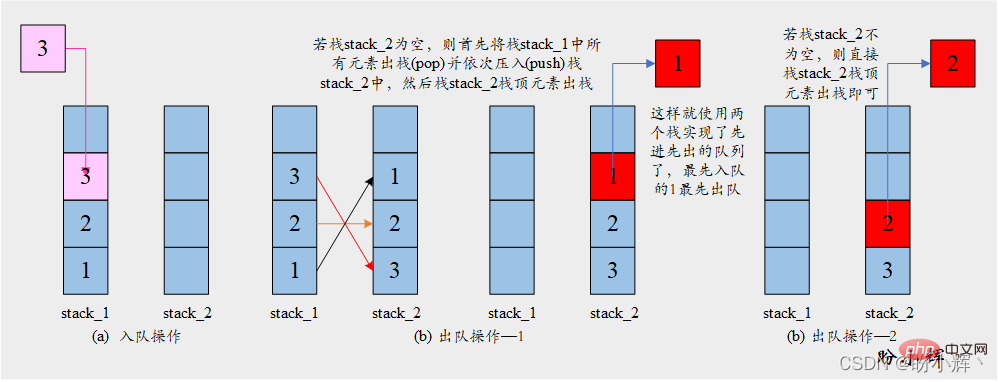
[算法]

 入队 enqueue：
   将元素推入栈 stack_1
 出队 dequeue：
   如果栈 stack_2 不为空：
     stack_2 栈顶元素出栈
   否则：
     将所有元素依次从 stack_1 弹出并压入 stack_2
     stack_2 栈顶元素出栈

[代码]

class Queue:
    def __init__(self):
        self.stack_1 = Stack()
        self.stack_2 = Stack()
    def enqueue(self, data):
        self.stack_1.push(data)
    def dequeue(self):
        if self.stack_2.isempty():
            while not self.stack_1.isempty():
                self.stack_2.push(self.stack_1.pop())
        return self.stack_2.pop()

[时空复杂度] 入队时间复杂度为$O(1)$，如果栈 stack_2 不为空，那么出队的时间复杂度为 $O(1)$，如果栈 stack_2 为空，则需要将元素从 stack_1 转移到 stack_2，但由于 stack_2 中转移的元素数量和出队的元素数量是相等的，因此出队的摊销时间复杂度为 $O(1)$。

2. 使用两个队列实现一个栈

[问题] 给定两个队列，仅使用队列的基本操作实现一个栈。

[思路] 由于队列并不具备反转顺序的特性，入队顺序即为元素的出队顺序。因此想要获取最后一个入队的元素，需要首先将之前所有元素出队。因此为了使用两个队列实现栈，我们需要将其中一个队列 store_queue 用于存储元素，另一个队列 temp_queue 则用来保存为了获取最后一个元素而保存临时出队的元素。push 操作将给定元素入队到存储队列 store_queue 中；pop 操作首先把存储队列 store_queue 中除最后一个元素外的所有元素都转移到临时队列 temp_queue 中，然后存储队列 store_queue 中的最后一个元素出队并返回。具体操作如下图所示：

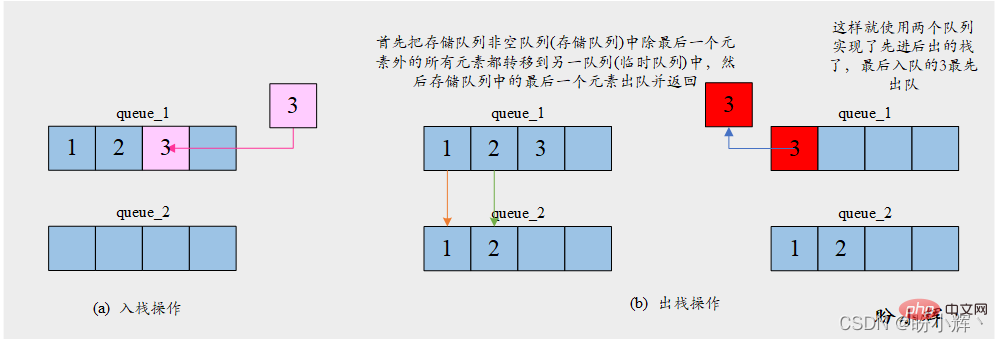
[算法]

 算法运行过程需要始终保持其中一个队列为空，用作临时队列
 入栈 push：在非空队列中插入元素 data。
   若队列 queue_1 为空：
     将 data 插入 队列 queue_2 中
   否则：
     将 data 插入 队列 queue_1 中
 出栈 pop：将队列中的前$n-1$ 个元素插入另一队列，删除并返回最后一个元素
   若队列 queue_1 不为空：
     将队列 queue_1 的前$n-1$ 个元素插入 queue_2，然后 queue_1 的最后一个元素出队并返回
   若队列 queue_2 不为空：
     将队列 queue_2 的前$n-1$ 个元素插入 queue_1，然后 queue_2 的最后一个元素出队并返回

[代码]

class Stack:
    def __init__(self):
        self.queue_1 = Queue()
        self.queue_2 = Queue()
    def isempty(self):
        return self.queue_1.isempty() and self.queue_2.isempty()
    def push(self, data):
        if self.queue_2.isempty():
            self.queue_1.enqueue(data)
        else:
            self.queue_2.enqueue(data)
    def pop(self):
        if self.isempty():
            raise IndexError("Stack is empty")
        elif self.queue_2.isempty():
            while not self.queue_1.isempty():
                p = self.queue_1.dequeue()
                if self.queue_1.isempty():
                    return p
                self.queue_2.enqueue(p)
        else:
            while not self.queue_2.isempty():
                p = self.queue_2.dequeue()
                if self.queue_2.isempty():
                    return p
                self.queue_1.enqueue(p)

[时空复杂度] push 操作的时间复杂度为$O(1)$，由于 pop 操作时，都需要将所有元素从一个队列转移到另一队列，因此时间复杂度$O(n)$。

3. 栈中元素连续性判断

[问题] 给定一栈 stack1，栈中元素均为整数，判断栈中每对连续的数字是否为连续整数(如果栈有奇数个元素，则排除栈顶元素)。例如，输入栈 [1, 2, 5, 6, -5, -4, 11, 10, 55]，输入为 True，因为排除栈顶元素 55 后，(1, 2)、(5, 6)、(-5, -4)、(11, 10) 均为连续整数。

[思路] 由于栈中可能存在奇数个元素，因此为了正确判断，首次需要将栈中元素反转，栈顶元素变为栈底，然后依次出栈，进行判断。

[算法]

 栈 stack 中所有元素依次出栈，并插入队列 queue 中
 队列 queue 中所有元素出队，并入栈 stack
  while 栈 stack 不为空：
   栈顶元素 e1 出栈，并插入队列 queue 中
   如果栈 stack 不为空：
     栈顶元素 e2 出栈，并插入队列 queue 中
     如果 |e1-e2|!=1：
       返回 False，跳出循环
 队列 queue 中所有元素出队，并入栈 stack

[代码]

def check_stack_pair(stack):
    queue = Queue()
    flag = True
    # 反转栈中元素
    while not stack.isempty():
        queue.enqueue(stack.pop())
    while not queue.isempty():
        stack.push(queue.dequeue())
    while not stack.isempty():
        e1 = stack.pop()
        queue.enqueue(e1)
        if not stack.isempty():
            e2 = stack.pop()
            queue.enqueue(e2)
            if abs(e1-e2) != 1:
                flag = False
                break
    while not queue.isempty():
        stack.push(queue.dequeue())
    return flag

[时空复杂度] 时间复杂度为$O(n)$，空间复杂度为$O(n)$。

4. 重新排列队列中元素顺序

[问题] 给定一个整数队列 queue，将队列的前半部分与队列的后半部分交错来重新排列元素。例如输入队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9]，则输出应为 [1, 6, 2, 7, 3, 8, 4, 9, 5]。

[思路] 通过获取队列的前半部分，然后利用栈的反转特性，可以实现重排操作，如下图所示：

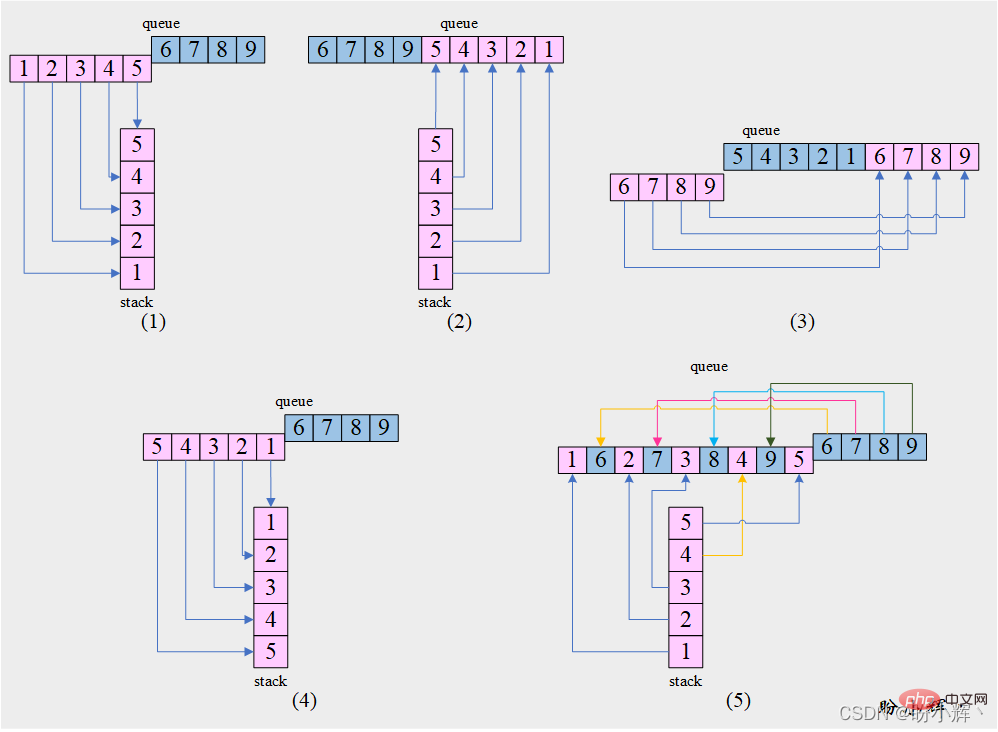
[算法]

 如果队列 queue 中的元素数为偶数：
   half=queue.size//2
 否则：
   half=queue.size//2+1
 1. 将队列 queue 的前半部分元素依次出队并入栈 stack
 2. 栈 stack 中元素出栈并入队 queue
 3. 将队列 queue 中在步骤 1中未出队的另一部分元素依次出队并插入队尾
 4. 将队列 queue 的前半部分元素依次出队并入栈 stack
 5. 将栈 stack 和队列 queue 中的元素交替弹出并入队
 6. 如果栈 stack 非空：
   栈 stack 中元素出栈并入队

[代码]

def queue_order(queue):
    stack = Stack()
    size = queue.size    if size % 2 == 0:
        half = queue.size//2
    else:
        half = queue.size//2 + 1
    res = queue.size - half    for i in range(half):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(res):
        queue.enqueue(queue.dequeue())
    for i in range(half):
        stack.push(queue.dequeue())
    for i in range(res):
        queue.enqueue(stack.pop())
        queue.enqueue(queue.dequeue())
    if not stack.isempty():
        queue.enqueue(stack.pop())

[时空复杂度] 时间复杂度为$O(n)$，空间复杂度为$O(n)$。

5. 反转队列中前 m 个元素的顺序

[问题] 给定一个整数 m 和一个整数队列 queue，反转队列中前 k 个元素的顺序，而其他元素保持不变。如 m=5，队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9]，算法输出为 [5, 4, 3, 2, 1, 6, 7, 8, 9]。

[思路] 结合 [问题4] 我们可以发现，此题就是 [问题4] 的前 3 步，如下图所示：

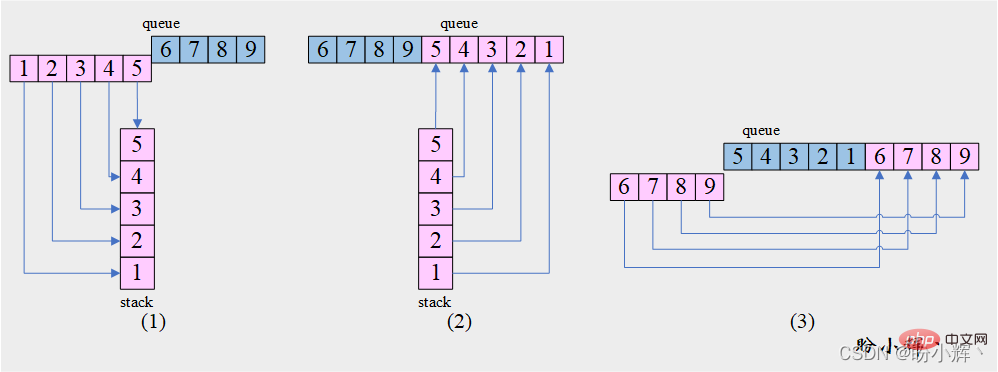
[算法]

 1. 将队列 queue 的前 m 个元素依次出队并入栈 stack
 2. 栈 stack 中元素出栈并入队 queue
 3. 将队列 queue 中在步骤 1中未出队的另一部分元素依次出队并插入队尾

[代码]

def reverse_m_element(queue, m):
    stack = Stack()
    size = queue.size    if queue.isempty() or m>size:
        return
    for i in range(m):
        stack.push(queue.dequeue())
    while not stack.isempty():
        queue.enqueue(stack.pop())
    for i in range(size-m):
        queue.enqueue(queue.dequeue())

[时空复杂度] 时间复杂度为$O(n)$，空间复杂度为 $O(n)$。

推荐学习：python教程

以上就是一起来分析Python队列相关应用与习题的详细内容，更多请关注zzsucai.com其它相关文章！